Как комфортно играть в шутеры на геймпаде?
Часть 1. Настройки- Хэй-йо, дамы и господа! На связи Сергей Borlader, некогда редактор портала про консольные видеоигры Stratege.ru, а ныне ведущий для него же подкаст «На краю вселенной». Я страсть как обожаю видеоигры. Хлебом не корми, дай понажимать кнопки, исследуя загадочные миры и сражаясь с могущественными боссами. Но есть в моей любви одна странноватая изюминка: сильнее иного меня поглощает игра в шутеры. Шутеры на геймпаде.
- Увлёкся этим ремеслом я более десяти лет назад и до сих пор не могу остановиться. Последние два года активно практикуюсь в мультиплеере, где добился ощутимого прогресса. Из личных достижений — звание «Высшего хищника», эмблемы за 20 убийств и 4 000 урона за матч в консольной версии Apex Legends, а также попадание в топ 1% игроков Call of Duty: Warzone с K/D 2.7 в кроссплее. За всё время успел перепробовать уйму геймпадов, платформ, модификаций и настроек, овладел методом хвата Клоу.

Начнём с того, что стандартные настройки обзора во всех консольных шутерах просто ужасны. Они предназначены скорее для неопытных новичков, впервые взявших в руки контроллер. Для тех же, кто хочет стать лучше, есть шанс на спасение, но придётся отказаться от старых привычек и едва ли не заново научиться играть.
Шаг 1. Мёртвая зона.
Мёртвая зона (англ. Dead Zone) — диапазон, в котором отклонения стика не регистрируются.
В идеальном мире мы бы выкрутили этот параметр в ноль, но это лишь утопия. Устройство современных 3D-аналогов изначально может допускать небольшое нарушение центровки стиков, что в свою очередь может привести к их дрифту.
Дрифт стика (англ. Drift — «дрейф») — нарушение центровки стика в нулевом положении, из-за чего отклонение 3D-аналога регистрируется даже в состоянии покоя. Это явление вызывает самовольное движение персонажа, либо камеры, в любом направлении.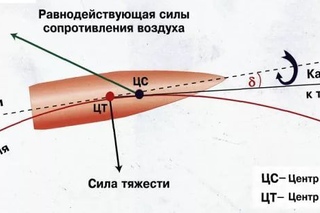 С износом механизма эффект усиливается. Обычно лечится чисткой потенциометров проблемного 3D-аналога либо полной его заменой.
С износом механизма эффект усиливается. Обычно лечится чисткой потенциометров проблемного 3D-аналога либо полной его заменой.
Чтобы скрыть этот изъян и были введены мёртвые зоны. Они зависят от конкретного экземпляра вашего геймпада и их размеры придётся подбирать самостоятельно. Стремитесь к минимуму, но так, чтобы прицел не вело в сторону без вашего ведома, и вы чётко могли его контролировать.
Чем меньше мёртвая зона, тем лучше!
Шаг 2. Чувствительность обзора.
Чувствительность обзора (англ. Look Sensitivity) — соотношение между степенью отклонения стика и смещением прицела в игре. Может называться чувствительностью джойстика, камеры, стика и так далее. Зачастую делится на два отдельных параметра: чувствительность по оси X и оси Y, но лучше сохранять эти значения одинаковыми, чтобы контроль стика был более интуитивным.
Чувствительность, как и вкусы, понятие индивидуальное. К ней нужен особый подход и выявить ту самую можно только путём долгих практических скитаний.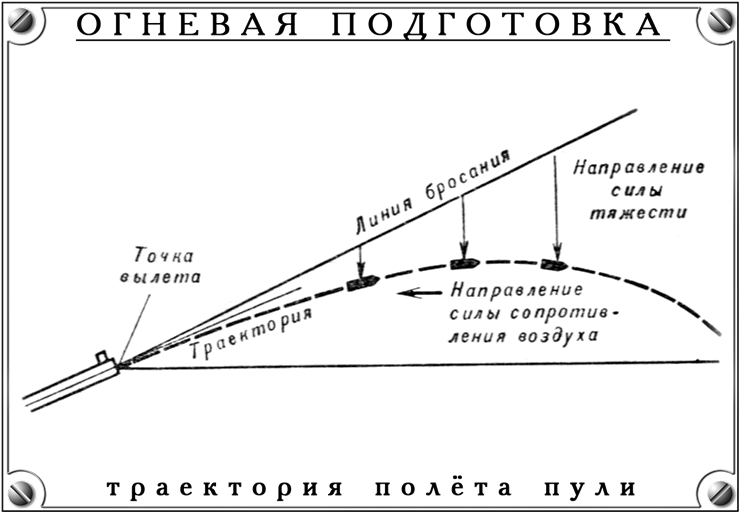
Чем выше чувствительность обзора, тем лучше!
Шаг 3. Кривая вывода.
Кривая вывода (англ. Output Curve) — график обработки входящих сигналов 3D-аналога, отвечающий за зависимость ускорения движения камеры от величины отклонения стика. Может также называться кривой отдачи, кривой отклика, типом реакции при прицеливании и тому подобными терминами. В современных играх обычно имеет несколько вариантов настройки, в ранних же проектах отсутствует вовсе.
С этой настройки начинаются тайные запретные знания, ведь правильный её выбор позволит немного приблизиться к точности компьютерной мыши. Кривых вывода существует огромное множество, но мы разберём только основные их типы.
Стандартная — замедление прицела при отклонении стика до середины и плавное снижение эффекта после. Совсем не отзывчиво и слабо эффективно. По сути, это отнимает больше половины хода стика, которая могла бы помочь в микродвижениях. Данная кривая вывода повсеместно используется разработчиками как непоколебимый стандарт, в том числе в тех играх, где этот параметр настроить нельзя.
Линейная — прямо пропорциональная зависимость скорости движения прицела от степени отклонения стика. Проще говоря, чем больше отклонение стика, тем выше скорость перемещения прицела. Линейная кривая вывода является наиболее оптимальной в подавляющем большинстве случаев.
Динамическая — постепенное ускорение прицела в первой половине хода стика и плавное замедление во второй. Может называться по-другому, пример взят из серии Call of Duty. Является отличным аналогом линейной кривой вывода, более чутким в микродвижениях.
Ваш выбор: линейная кривая и её аналоги. В таком случае вы получаете возможность как быстро развернуться на 180 градусов, так и с комфортом довести прицел на голову врага из снайперской винтовки. Все параметры, отвечающие за замедление прицела, вроде сглаживания при обзоре из Doom Eternal, надо отключить, чтобы контроль прицела был более интуитивным.
В таком случае вы получаете возможность как быстро развернуться на 180 градусов, так и с комфортом довести прицел на голову врага из снайперской винтовки. Все параметры, отвечающие за замедление прицела, вроде сглаживания при обзоре из Doom Eternal, надо отключить, чтобы контроль прицела был более интуитивным.
Кривая вывода должна быть линейной или аналогичной ей!
Шаг 4. Помощь в прицеливании.
Помощь в прицеливании (англ. Aim Assist) — алгоритм, корректирующий процесс стрельбы игрока для получения наиболее комфортного игрового опыта. Широко применяется как для управления с геймпада, так и с компьютерной мыши. В современных шутерах делится на два основных типа: прилипание и магнетизм пуль. Прилипание замедляет перекрестье прицела при приближении к врагу, а магнетизм немного корректирует траекторию полёта пули, чтобы попадания казались честными по отношению к игроку. Первый тип используется в основном для геймпада, а второй для обоих видов игровых манипуляторов.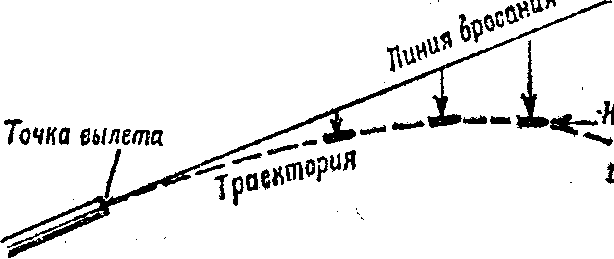
Поведение помощи в прицеливании зависит от конкретной игры. Если говорить про мультиплеерные проекты, то это зачастую едва заметное замедление прицела рядом с врагом, но в одиночных и некоторых несерьёзных многопользовательских играх встречается также вариант автоприцеливания (англ. Auto Aim), которое автоматически наводит прицел на врага.
Вопреки обличающим речам многих адептов клавиатуры и мыши, в мультиплеере большинства шутеров помощь в прицеливании выражена слабо. Иногда она даже мешает, цепляясь за нокаутированных врагов. Однако раз в год и палка стреляет, а потому если помощь работает адекватно, то её лучше оставить. Работу ассистента вы вряд ли заметите, но играть будет немного комфортнее.
Если помощь в прицеливании не мешает, то её лучше не отключать!
Шаг 5. Поле зрения.
Поле зрения (англ. FOV — Field of View) — угловое пространство, видимое игровой камерой в один момент времени. Чем выше угол поля зрения, тем большая область пространства одномоментно выводится на экран игрока. Стандартное значение этого параметра около 70°, максимальное порядка 120°. При высоких значениях камера будто бы отдаляется, из-за чего модельки врагов в центре экрана становятся меньше. По той же причине чувствительность обзора кажется более медленной, а скорость перемещения наоборот — быстрой.
Чем выше угол поля зрения, тем большая область пространства одномоментно выводится на экран игрока. Стандартное значение этого параметра около 70°, максимальное порядка 120°. При высоких значениях камера будто бы отдаляется, из-за чего модельки врагов в центре экрана становятся меньше. По той же причине чувствительность обзора кажется более медленной, а скорость перемещения наоборот — быстрой.
Большие значения этого параметра могут отрицательно (но не критично) повлиять на FPS, из-за того, что с расширением видимой области увеличивается и зона рендера.
Подход в выборе правильного поля зрения аналогичен чувствительности обзора. Стремитесь к максимуму, но не забывайте про комфортный предел. Да, модельки врагов станут мельче, но так вы будете лучше видеть, что происходит вокруг, и вам станет проще контролировать окружающую обстановку.
Чем больше поле зрения, тем лучше!
Шаг 6. Размытие в движении.
Размытие в движении (англ.
Самое злостное зло, которое можно придумать для шутера. Экран размывается при перемещении прицела и разглядеть что-либо в этот момент практически невозможно. Если размытие в движении можно отключить, делайте это немедля. Сюда относятся и другие эффекты, вроде аберраций, зернистости, дополнительной тряски камеры и всего того, что может помешать обзору. В одиночных проектах что-то можно и оставить, главное не забывать о собственном комфорте.
Размытие в движении и другие эффекты, ухудшающие видимость, необходимо отключить!
На этом с настройками — всё. Материал получился большой и основательный, потому было решено разделить его на две части. В сиквеле вас ждёт ворох полезной информации о девайсах: геймпадах, стиках, лепестках, дисплеях, наушниках и тому подобном стаффе. Выход продолжения себя долго ждать не заставит! А пока можете сходить в гости ко мне в Twitter и подписаться на только-только созданный YouTube-канал, чтобы узнавать больше о технике геймпадного аима в будущем. Сайонара! Увидимся через несколько дней!
Сайонара! Увидимся через несколько дней!
Читать Часть 2.
2.3.1 Траектория полета пули
2.3.1 Траектория полета пули2.3.1 Траектория полета пули
Пуля, получив при вылете из канала ствола определенную начальную скорость, стремится по инерции сохранить величину и направление этой скорости. Если бы полет пули проходил в безвоздушном пространстве и на нее не действовала сила тяжести, пуля двигалась бы прямолинейно, равномерно и бесконечно. Однако на пулю, летящую в воздушной среде, действуют силы, которые изменяют скорость полета и направление движения. Этими силами являются сила тяжести и сила сопротивления воздушной среды (рис. 34).
Рис. 34 — Силы, действующие на пулю во время ее полета
В результате совместного действия этих двух сил пуля теряет скорость и изменяет направление своего движения, перемещаясь по кривой линии, проходящей ниже направления оси канала ствола.
Линия, которую описывает в пространстве центр тяжести движущейся пули (снаряда), называется траекторией.
Баллистика рассматривает траекторию над (или под) горизонтом оружия — воображаемой бесконечной горизонтальной плоскостью, проходящей через точку вылета (рис. 35).
Рис. 35 — Горизонт оружия
Движение пули, а следовательно, и форма траектории зависят от многих условий. Поэтому необходимо прежде всего рассмотреть, как действуют на пулю в отдельности сила тяжести и сила сопротивления воздушной среды.
Действие силы тяжести. Представим, что на пулю, вылетевшую из канала ствола, не действует никакая сила. В таком случае она двигалась бы по инерции бесконечно, равномерно и прямолинейно по направлению оси канала ствола и за каждую секунду пролетала бы одинаковые расстояния с постоянной скоростью, равной начальной. Тогда, если бы ствол оружия был направлен прямо в цель, пуля, следуя в направлении оси канала ствола, непременно попала бы в нее (рис. 36).
Рис. 36 — Движение пули по инерции (если бы не было силы тяжести и сопротивления воздуха)
Допустим теперь, что на пулю действует только одна сила тяжести.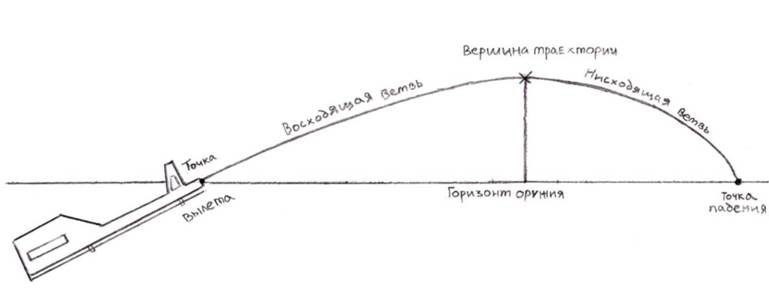 Тогда она, как и всякое свободно падающее тело, начнет падать вертикально вниз.
Тогда она, как и всякое свободно падающее тело, начнет падать вертикально вниз.
Как известно из механики, высота падения
H = gt2 / 2где g — ускорение силы тяжести (9,8 м/сек2), t — время в секундах.
Так, за 1 сек. пуля упадет вниз на 9,8*12 / 2 = 4,9 м, за 2 сек. — 9,8*22 / 2 = 19,6 м, за 3 сек. — 44,1 м, за 4 сек. — 78,4 м и т.д. (рис. 37).
Рис. 37 — Падение пули (в пустоте) под действием силы тяжести
Если предположить, что во время полета по инерции в безвоздушном пространстве на пулю действует сила тяжести, то под ее действием пуля опустится ниже линии продолжения оси канала ствола в первую секунду на 4,9 м, во вторую — на 19,6 м и т.д. Тогда, если навести оружие на цель, пуля пролетит под целью (рис. 38).
Рис. 38 — Движение пули (если бы на нее действовала сила тяжести, но не действовало сопротивление воздуха)
Поэтому, чтобы пуля пролетела определенное расстояние и попала в цель, необходимо направить ствол оружия куда-то выше цели.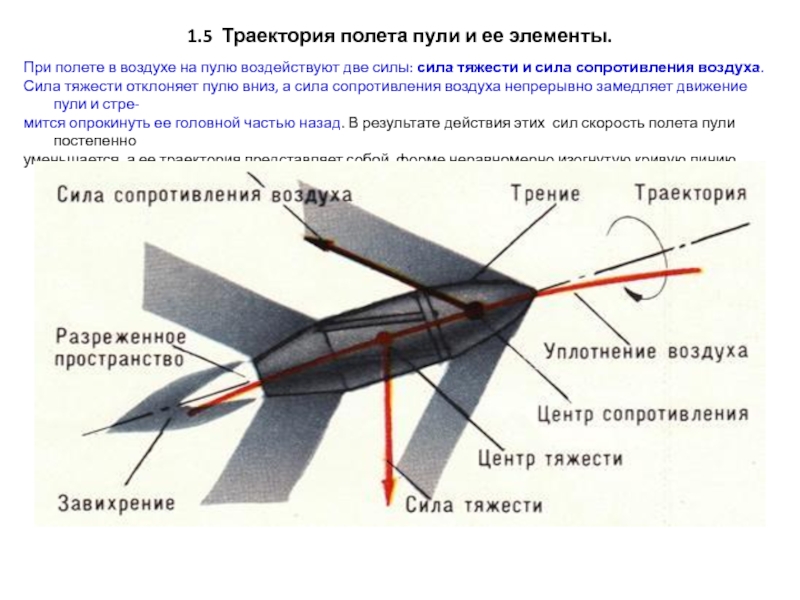 Для этого нужно, чтобы ось канала ствола и плоскость горизонта оружия составляли некоторый угол, который называется углом возвышения (рис. 39).
Для этого нужно, чтобы ось канала ствола и плоскость горизонта оружия составляли некоторый угол, который называется углом возвышения (рис. 39).
Рис. 39 — Угол возвышения (траектория пули в безвоздушном пространстве)
Как видно на рис. 39, траектория пули в безвоздушном пространстве, на которую действует сила тяжести, представляет собой правильную кривую — параболу. Самая высокая точка траектории над горизонтом оружия называется ее вершиной. Часть кривой от точки вылета до вершины называется восходящей ветвью. Такая траектория отличается тем, что восходящая и нисходящая ветви совершенно одинаковы, а угол бросания и угол падения равны.
Действие силы сопротивления воздушной среды. На первый взгляд кажется маловероятным, чтобы воздух, обладающий столь малой плотностью, мог оказывать существенное сопротивление движению пули и тем самым значительно уменьшать ее скорость.
Однако опыты показали, что сила сопротивления воздуха, действующего на пулю, выпущенную из 7,62-мм винтовки, составляет большую величину — 3,5 кг.
Поскольку пуля весит всего лишь несколько граммов, становится очевидным большое тормозящее действие, которое оказывает воздух на летящую пулю.
Во время полета пуля расходует значительную часть своей энергии, чтобы раздвинуть частицы воздуха. Снимок пули, летящей со сверхзвуковой скоростью (свыше 340 м/сек), показывает, что перед ее головной частью образуется уплотнение воздуха (рис. 40). От этого уплотнения расходится во все стороны головная баллистическая волна. Частицы воздуха, скользя по поверхности пули и срываясь с ее боковых стенок, образуют сзади пули зону разреженного пространства. Стремясь заполнить образовавшуюся пустоту, частицы воздуха создают завихрения, в результате чего за пулей тянется хвостовая волна.
Рис. 40 — Фотоснимок пули, летящей со сверхзвуковой скоростью (свыше 340 м/сек)
Уплотнение воздуха впереди головной части пули тормозит ее полет, разреженная зона сзади засасывает ее и еще больше усиливает торможение; стенки пули испытывают трение о частицы воздуха, что также замедляет ее полет.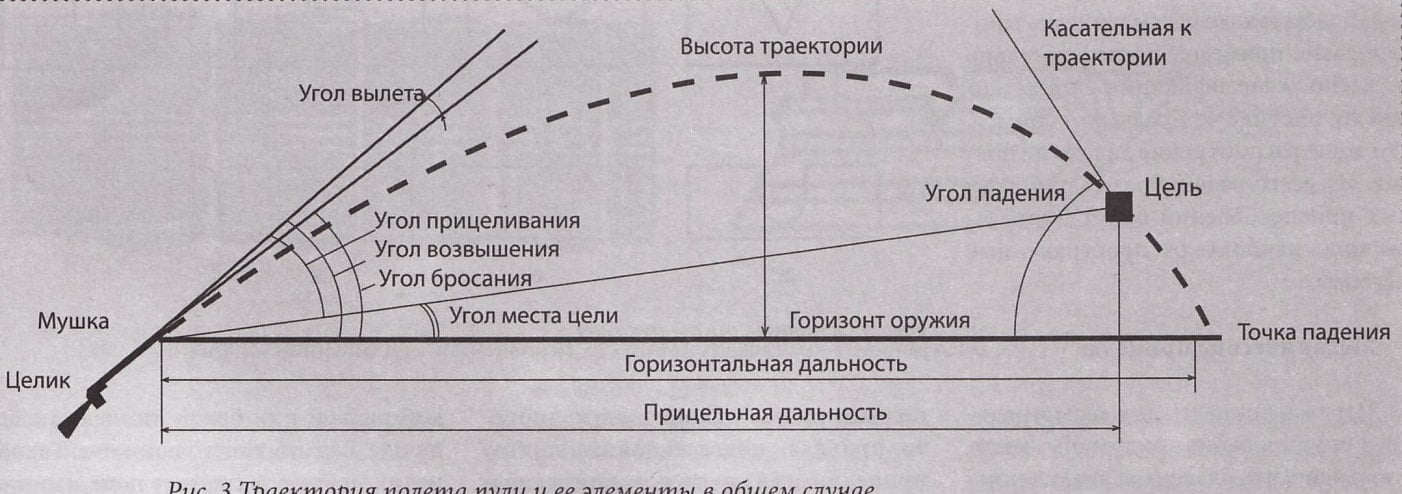 Равнодействующая этих трех сил и составляет силу сопротивления воздуха. Насколько велико действие сопротивления воздуха на полет пули, можно судить по графику, изображенному на рис. 41.
Равнодействующая этих трех сил и составляет силу сопротивления воздуха. Насколько велико действие сопротивления воздуха на полет пули, можно судить по графику, изображенному на рис. 41.
Рис. 41 — Окончательная скорость легкой и тяжелой пуль при стрельбе из 7,62-мм служебной винтовки
Следовательно, под действием силы сопротивления воздуха траектория пули теряет форму правильной параболы — теперь она выглядит несимметричной кривой: вершина делит ее на две неравные части, причем восходящая ветвь всегда длиннее и отложе нисходящей. При стрельбе на средние дистанции можно условно принимать соотношение длины восходящей ветви траектории к нисходящей как 3:2.
Урок ОБЖ на тему «Полет пули и элементы ее траектории»
Тема: Полет пули и элементы ее траектории.
Утверждаю ____________
Директор МОБУ СОШ №1 с Инзер
Цели:
1. объяснить практическое значение знания траектории полета пули.
2. ознакомить учащихся с элементами траектории полета пули.
3. воспитывать ответственное отношение к предмету.
Метод: рассказ с показом
Оборудование: таблицы и схемы «траектория полета пули», макет автомата.
План урока
1. Орг. момент. 3мин.
Доклад командира взвода, проверка внешнего вида учащихся.
Путем опроса установить усвоение ранее изученного материала.
Объявить тему и цель занятия.
2. Объяснение нового материала 35 мин
Отдача оружия (5мин)
Полет пули в воздухе (30мин)
Образование линии полета
Траектория полета пули
Элементы траектории, термины
Прямой выстрел, его практическое значение
3. Закрепление 2мин
4. Домашнее задание: подготовиться по конспекту.
Домашнее задание: подготовиться по конспекту.
Конспект урока
Отдача оружия
Давление газов в канале ствола действует во все стороны с одинаковой силой. Оно выталкивает пулю вперед, а оружие отталкивает назад. Под действием пороховых газов на дно гильзы, плотно запертой затвором в канале ствола, ствол и связанные с ним части оружия двигаются в сторону, обратную направлению движения пули. Это движение оружия назад во время выстрела называется отдачей. Скорость и энергия отдачи оружия примерно во столько раз меньше начальной скорости и энергии пули, во сколько раз пуля легче оружия. Энергия отдачи у ручного стрелкового оружия обычно не превышает 2 кгм и воспринимается стреляющим безболезненно.
Сила давления пороховых газов, вызывающая отдачу оружия, действует по оси канала ствола и встречает сопротивление в виде упора приклада в плечо стрелка. Точка приложения силы сопротивления (соприкосновения затыльника приклада, с плечом стреляющего) находится ниже направления силы отдачи. В результате образуется пара сил, которая вращает оружие, приподнимая ствол кверху.
В результате образуется пара сил, которая вращает оружие, приподнимая ствол кверху.
Кроме того, вследствие большого давления и высокой температуры пороховых газов, а также трения пули при движении по нарезам стенки ствола испытывают колебания (вибрируют) подобно звучащей струне. Это также заставляет дульную часть ствола смещаться от первоначального положения.
В результате взаимодействия этих причин пуля полетит не в направлении оси канала ствола, которое было ему придано до выстрела (при наводке), а в том направлении, какое займет ось канала ствола в момент вылета из него пули. Таким образом, между направлением оси канала ствола до выстрела и ее направлением в момент вылета пули образуется угол, который называется углом вылета. Его величина имеет практическое значение и зависит от изготовки стрелка.
Достаточно при изготовке переместить кисть левой руки по цевью вперед или назад, как величина угла вылета изменится, и пули пойдут соответственно ниже или выше. Изменяется величина угла вылета также от положения приклада в плече. Если приклад упереть в плечо верхней частью затыльника, то угол вылета уменьшится и пули пойдут вниз, а если приклад упереть нижней частью затыльника, то угол вылета увеличится, нули пойдут вверх.
Изменяется величина угла вылета также от положения приклада в плече. Если приклад упереть в плечо верхней частью затыльника, то угол вылета уменьшится и пули пойдут вниз, а если приклад упереть нижней частью затыльника, то угол вылета увеличится, нули пойдут вверх.
Образование угла вылета (При стрельбе из малокалиберной винтовки угол вылета положительный)
Для того чтобы сохранить более или менее постоянную величину угла вылета, каждый стреляющий должен настойчиво вырабатывать однообразное выполнение всех элементов изготовки.
Отсутствие однообразия в изготовке вызывает колебание в величине углов вылета и увеличивает отклонение пуль от точки прицеливания по высоте.
Полет пули в воздухе.
В момент выстрела ствол оружия занимает определенное положение. Прямая линия, представляющая собой продолжение оси канала ствола в момент вылета пули, называется линией бросания.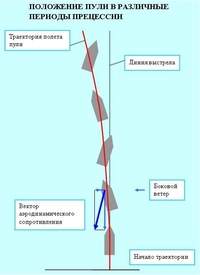
При движении в воздухе пуля подвергается действию силы тяжести и силы сопротивления воздуха. Сила тяжести направлена вниз и заставляет пулю непрерывно понижаться от линии бросания. Действие силы сопротивления воздуха направлено навстречу движению пули и заставляет ее непрерывно терять скорость полета.
Под действием этих двух сил пуля летит в воздухе не по прямой, в направлении которой она была выброшена из канала ствола (линии бросания), а по кривой, неравномерно изогнутой линии, расположенной ниже линии бросания . Кривая линия, которую описывает центр тяжести пули (гранаты) при полете в воздухе, называется траекторией.
Началом траектории является точка вылета пули (центр дульного среза ствола), концом — точка встречи (точка пересечения траектории с поверхностью цели, преграды или земли).
Траектория полета пули (рис)
Кратчайшее расстояние от любой точки траектории до линии прицеливания называется превышением траектории над линией прицеливания.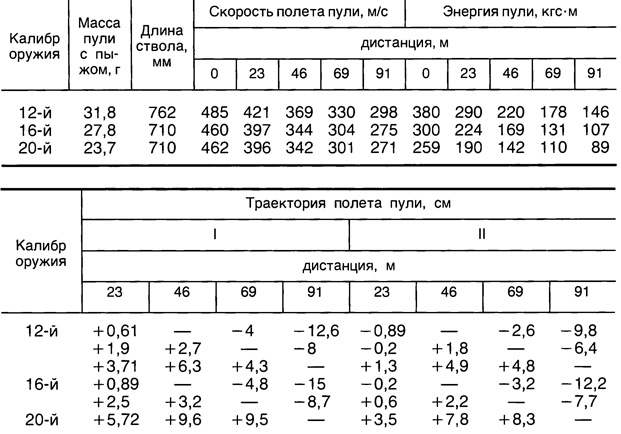
Точку пересечения траектории с горизонтом оружия принято называть точкой падения.
Расстояние от точки вылета до точки падения пули представляет собой полную горизонтальную дальность.
Скорость пули (гранаты) в точке падения называется окончательной скоростью.
Время движения пули (гранаты) от точки вылета до точки падения называется полным временем полета. Кратчайшее расстояние от вершины траектории до горизонта оружия является высотой траектории.
Угол, заключенный между касательной к траектории в точке падения и горизонтом оружия, называется углом падения.
В результате одновременного воздействия на пулю вращательного движения, придающего ей устойчивое положение в полете (по принципу гироскопа), и сопротивления воздуха, стремящегося опрокинуть ее головкой назад, ось пули отклоняется от направления полета в сторону вращения. Вследствие этого пуля встречает сопротивление воздуха больше одной своей стороной и поэтому еще больше отклоняется от плоскости стрельбы в сторону вращения. Такое отклонение пули в сторону от плоскости стрельбы называется деривацией. Траектория вращающейся пули в плане представляет собой также кривую линию . При правой нарезке ствола деривация всегда происходит в правую сторону от плоскости стрельбы.
Такое отклонение пули в сторону от плоскости стрельбы называется деривацией. Траектория вращающейся пули в плане представляет собой также кривую линию . При правой нарезке ствола деривация всегда происходит в правую сторону от плоскости стрельбы.
Деривация пули (вид сверху)
При стрельбе по самолетам вертикально вверх (угол бросания 90°) вследствие отсутствия опрокидывающего момента в действии сопротивления воздуха деривация отсутствует.
Наводка и ее элементы.
Теперь, когда мы ознакомились с движениям пули в воздухе нетрудно понять, что если цель будет находиться на линии продолжения оси канала ствола, то пуля в нее не попадет, а упадет ниже. Это произойдет потому, что пуля в силу своей тяжести за время полета до цели опустится от приданного ей первоначального направления. Для того чтобы поразить цель, необходимо ось канала ствола оружия направить выше точки, в которую мы хотим попасть, причем настолько выше, насколько пуля за время своего полета до цели опустится ниже линии бросания.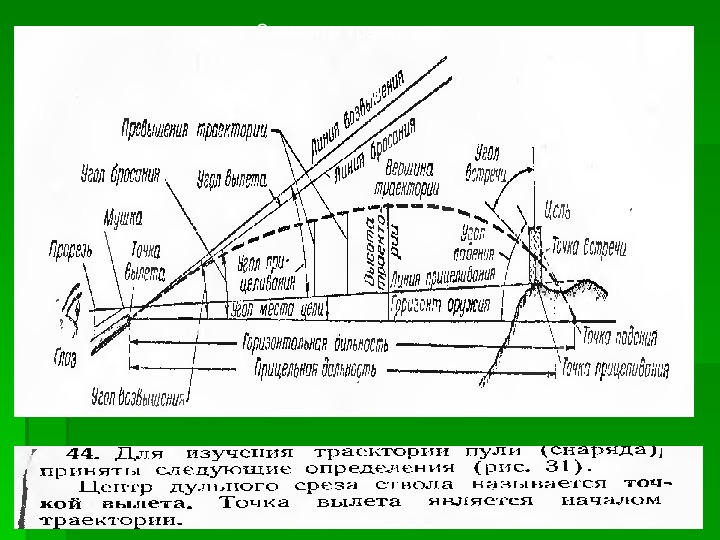
Надо иметь в виду, что чем больше расстояние до цели, тем больше времени пуля затратит на полет и тем на большую величину она опустится. При большей дальности стрельбы необходимо придавать больший угол возвышения стволу.
Однако сделать это на глаз невозможно; выполняется это с помощью прицела. Он устроен так, что если поставить хомутик на деление, соответствующее расстоянию до цели, и правильно прицелиться, то при выстреле пуля будет выброшена из канала ствола выше цели как раз настолько, насколько она опустится за время своего полета до цели. Следовательно, чем больше расстояние до цели, тем больший прицел устанавливается.
Чтобы направить пулю в цель, необходимо после установки прицела на нужное деление придать оси канала ствола определенное направление в горизонтальной и вертикальной плоскостях. Действия, выполняемые при этом, называются наводкой, или прицеливанием.
Придание оси канала ствола требуемого положения в горизонтальной плоскости называется горизонтальной наводкой.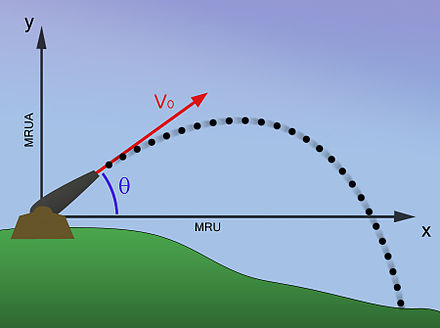 Она выполняется путем совмещения мушки с серединой прорези прицельной планки и направления оружия в таком положении в цель.
Она выполняется путем совмещения мушки с серединой прорези прицельной планки и направления оружия в таком положении в цель.
Придание оси канала ствола определенного положения в вертикальной плоскости называется вертикальной наводкой. Она выполняется путем выравнивания вершины мушки с краями гривки прорези и совмещения ее с точкой прицеливания.
Таким образом, горизонтальная и вертикальная наводки выполняются с помощью прицельных приспособлений.
Точка, в которую наводится оружие, называется точкой прицеливания (наводки) . В зависимости от высоты цели и дальности стрельбы ее выбирают в середине нижнего обреза цели, в центре ее или вне ее пределов.
Линия, идущая от глаза стрелка через середину прорези прицела на уровне с ее краями и вершину мушки в точку прицеливания, является линией прицеливания.
Прямая линия, соединяющая середину прорези прицела с вершиной мушки, называется прицельной линией.
Угол, образуемый линией прицеливания и линией возвышения, представляет собой угол прицеливания.
Точка пересечения нисходящей ветви траектории с линией прицеливания называется точкой падения.
Расстояние от точки вылета до пересечения траектории с линией прицеливания принято называть прицельной дальностью.
Между касательной к траектории в точке падения и линией прицеливания заключен угол падения.
Элементы траектории относительно линии прицеливания
Прямой выстрел и его практическое значение.
Это выстрел при котором траектория не поднимается над линией прицеливания выше цели на протяжении всего выстрела. Дальность прямого выстрела зависит от высоты цели и настильности траектории. Чем выше цель и настильнее траектория, тем больше дальность прямого выстрела и тем на большем удалении цель может быть поражена с одной установки прицела.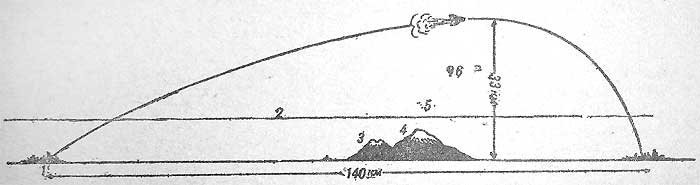
3. Закрепление 2мин
Вопросы для повторения:
1. Как происходит выстрел из огнестрельного оружия?
2. Влиянию каких сил подвергается пуля при полете в воздухе?
3. Какая ветвь траектории короче и круче и почему?
4. Почему угол бросания меньше угла падения?
5. Где скорость пули меньше — в точке вылета или в точке падения? Почему?
6. По какой ветви траектории время движения пули меньше?
7. Какую кривизну имеет траектория?
8. Что называется наводкой и из каких элементов она слагается?
4. Домашнее задание: подготовиться по конспекту.
Баллистика
- Подробности
- Категория: Снайпер
- Дата публикации 21.06.2013 18:01
- Автор: Super User
- Просмотров: 50631
Для успешного освоения техники стрельбы из любого стрелкового оружия, необходимо хорошо усвоить знания законов баллистики и ряда основных связанных с ней понятий. Без этого не обходился и не обходится ни один снайпер, без изучения этой дисциплины курс обучения снайпингу малополезен.
Без этого не обходился и не обходится ни один снайпер, без изучения этой дисциплины курс обучения снайпингу малополезен.
Баллистика — это наука о движении пуль и снарядов, выпущенных из стрелкового оружия при выстреле. Баллистика подразделяется на внешнюю и внутреннюю.
Внутренняя баллистика
Внутреняя баллистика изучает процессы, происходящие в канале ствола оружия во время выстрела, движение пули по каналу ствола и сопровождающих это явление -аэро и -термодинамических зависимостей как в канале ствола, так и за его пределами до окончания последействия пороховых газов.
Кроме того, внутренняя баллистика изучает вопросы наиболее рационального использования энергии порохового заряда во время выстрела с тем, чтобы пуле заданного калибра и веса сообщить оптимальную начальную скорость при соблюдении прочности ствола оружия: это дает исходные данные как для внешней баллистики, так и для проектирования оружия.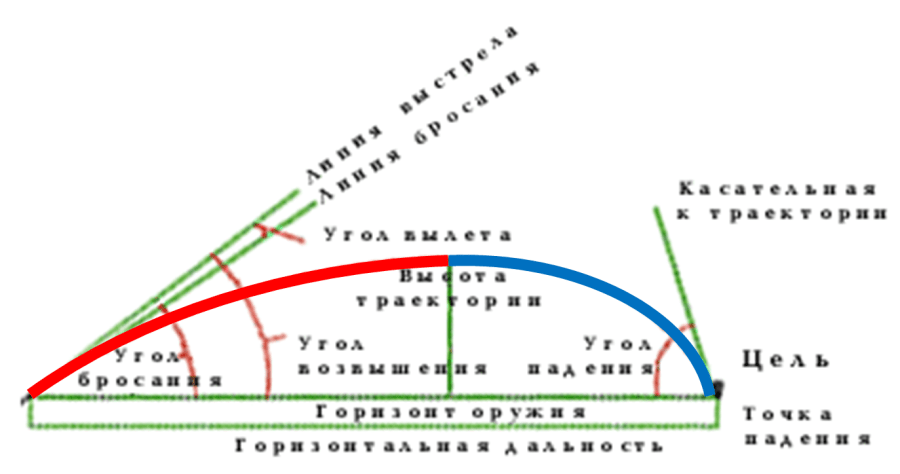
Выстрел
Выстрел — это выбрасывание пули из канала ствола оружия под воздействием энергии газов, образующихся при сгорании порохового заряда патрона.
Динамика выстрела. При ударе бойка по капсюлю боевого патрона, досланного в патронник, ударный состав капсюля взрывается, при этом, образуется пламя, которое через затравочные отверстия в дне гильзы передается пороховому заряду и воспламеняет его. При одномоментном сгорании боевого (порохового) заряда, образуется большое количество нагретых пороховых газов, которые создают высокое давление на дно пули, дно и стенки гильзы, а также на стенки канала ствола и затвор.
Под сильным давлением пороховых газов на дно пули, она отделяется от гильзы и врезается в каналы (нарезы) ствола оружия и, вращаясь по ним с постоянно нарастающей скоростью, выбрасывается наружу по направлению оси канала ствола.
В свою очередь, давление газов на дно гильзы вызывает движение оружия (ствола оружия) назад: это явление называют отдачей.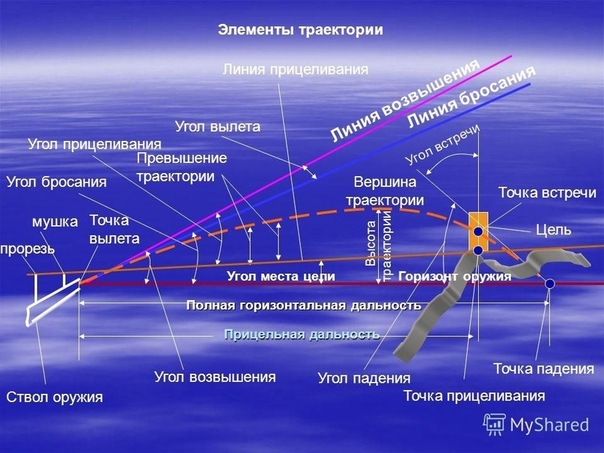 Чем больше калибр оружия и, соответственно, боеприпаса (патрона) под него — тем больше сила отдачи (смотрите ниже).
Чем больше калибр оружия и, соответственно, боеприпаса (патрона) под него — тем больше сила отдачи (смотрите ниже).
При выстреле из автоматического оружия, принцип действия которого основан на использовании отводимых через отверстие в стенке ствола энергии пороховых газов, как например в СВД, часть пороховых газов после прохождения в газовую камеру ударяет в поршень и отбрасывает толкатель с затвором назад.
Выстрел происходит в сверхкороткий промежуток времени: от 0,001 до 0,06 секунды и делится на четыре последовательных периода:
- предварительный
- первый (основной)
- второй
- третий (период последействия пороховых газов)
Внутренняя баллистика: выстрел, четыре периода выстрела
Предварительный период выстрела. Длится с момента возгорания порохового заряда патрона до момента полного врезания пули в нарезы канала ствола. На протяжении этого периода, в канале ствола создается давление газов достаточное для того, чтобы сдвинуть пулю с места и преодолеть сопротивление ее оболочки врезанию в нарезы канала ствола.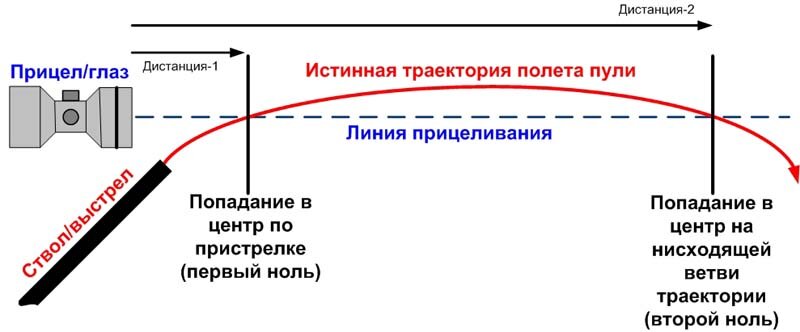 Такой тип давления называется давлением форсирования, которое достигает значения 250 — 600 кг/см² в зависимости от веса пули, твердости ее оболочки, калибра, типа ствола, количества и типа нарезов.
Такой тип давления называется давлением форсирования, которое достигает значения 250 — 600 кг/см² в зависимости от веса пули, твердости ее оболочки, калибра, типа ствола, количества и типа нарезов.
Первый (основной) период выстрела. Длится от момента начала движения пули по каналу ствола оружия до момента полного сгорания порохового заряда патрона. В этот период, горение порохового заряда происходит в быстро изменяющихся объемах: в начале периода, когда скорость движения пули по каналу ствола еще относительно невелика, количество газов растет быстрее, чем объем запульного пространства (пространство между дном пули и дном гильзы), давление газов быстро повышается и достигает наибольшей величины — 2900 кг/см² для 7,62 мм винтовочного патрона: это давление называется максимальным давлением. Оно создается у стрелкового оружия при прохождении пулей 4 — 6 см пути.
Затем, вследствие очень быстрого увеличения скорости движение пули, объем запульного пространства увеличивается быстрее притока новых газов, вследствие чего давление начинает падать: к концу периода оно равно приблизительно 2/3 максимального давления. Скорость движения пули постоянно возрастает и к концу периода достигает приблизительно 3/4 начальной скорости. Пороховой заряд полностью сгорает незадолго до того, как пуля вылетит из канала ствола.
Скорость движения пули постоянно возрастает и к концу периода достигает приблизительно 3/4 начальной скорости. Пороховой заряд полностью сгорает незадолго до того, как пуля вылетит из канала ствола.
Второй период выстрела. Длится с момента полного сгорания порохового заряда до момента вылета пули из канала ствола. С началом этого периода, приток пороховых газов прекращается, но сильно нагретые, сжатые газы расширяются и, оказывая давление на пулю — значительно увеличивают скорость ее движения. Спад давления во втором периоде происходит достаточно быстро и дульное давление у дульного среза ствола оружия составляет у различных образцов оружия 300 — 1000 кг/см². Дульная скорость, то есть скорость пули в момент вылета ее из канала ствола несколько меньше начальной скорости.
Третий период выстрела (период последействия пороховых газов). Длится от момента вылета пули из канала ствола оружия до момента прекращения действия пороховых газов на пулю. В течение этого периода пороховые газы, истекающие из канала ствола со скоростью 1200-2000 м/с, продолжают действовать на пулю и сообщают ей дополнительную скорость. Максимальной скорости пуля достигает в конце третьего периода на удалении нескольких десятков сантиметров от дульного среза ствола оружия. Этот период заканчивается в тот момент, когда давление пороховых газов на дно пули будет полностью уравновешено сопротивлением воздуха.
В течение этого периода пороховые газы, истекающие из канала ствола со скоростью 1200-2000 м/с, продолжают действовать на пулю и сообщают ей дополнительную скорость. Максимальной скорости пуля достигает в конце третьего периода на удалении нескольких десятков сантиметров от дульного среза ствола оружия. Этот период заканчивается в тот момент, когда давление пороховых газов на дно пули будет полностью уравновешено сопротивлением воздуха.
Начальная скорость пули
Начальная скорость пули — это скорость движения пули у дульного среза ствола оружия. За значение начальной скорости пули принимается условная скорость которая меньше максимальной, но больше дульной, что определяется опытным путем и соответствующими расчетами.
Этот параметр является одной из важнейших характеристик боевых свойств оружия. Величина начальной скорости пули указывается в таблицах стрельбы и в боевых характеристиках оружия. При увеличении начальной скорости увеличивается дальность полета пули, дальность прямого выстрела, убойное и пробивное действие пули, а также уменьшается влияние внешних условий на ее полет. Величина начальной скорости пули зависит от:
Величина начальной скорости пули зависит от:
- веса пули
- длины ствола
- температуры, веса и влажности порохового заряда
- размеров и формы зерен пороха
- плотности заряжания
Вес пули. Чем он меньше, тем больше ее начальная скорость.
Длина ствола. Чем она больше, тем больший промежуток времени пороховые газы действуют на пулю, соответственно, тем больше ее начальная скорость.
Температура порохового заряда. С понижением температуры, начальная скорость пули уменьшается, с повышением — увеличивается в связи с увеличением скорости горения пороха и значением давления. При нормальных погодных условиях, температура порохового заряда примерно равна температуре воздуха.
Вес порохового заряда. Чем больше вес порохового заряда патрона, тем большее воличество пороховых газов, воздействующих на пулю, тем большее давление в канале ствола и, соответственно — скорость полета пули.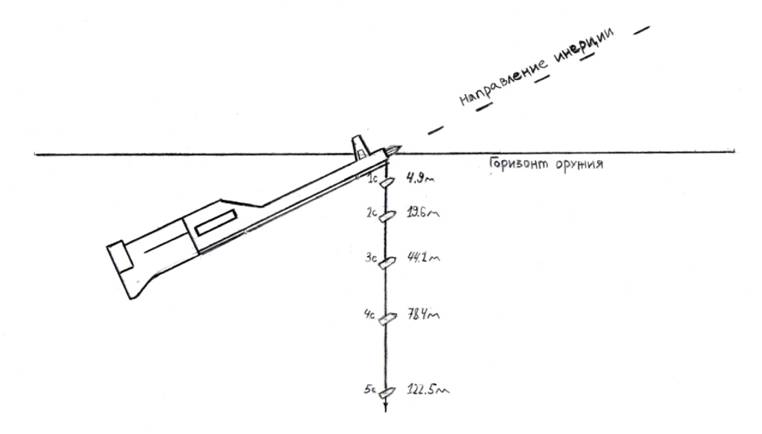
Влажность порохового заряда. При ее повышении, уменьшается скорость горения пороха, соответственно, скорость пули снижается.
Размеры и форма зерен пороха. Зерна пороха различных размеров и формы имеют разную скорость горения, а это оказывает существенное влияние на начальную скорость пули. Оптимальный вариант подбирается на стадии разработки оружия и при его последующих испытаниях.
Плотность заряжания. Это соотношение веса порохового заряда к объему гильзы патрона при вставленной пуле: это пространство называется камерой сгорания заряда. При слишком глубокой посадке пули в гильзу патрона значительно увеличивается плотность заряжания: при выстреле, это может привести к разрыву ствола оружия вследствие резкого скачка давления внутри него, потому такие патроны нельзя использовать для стрельбы. Чем больше плотность заряжания — тем меньше начальная скорость пули, чем меньше плотность заряжания — тем больше начальная скорость пули.
Отдача
Отдача — это движение оружия назад в момент выстрела. Ощущается в виде толчка в плечо, руку, грунт или комбинации этих ощущений. Действие отдачи оружия примерно во столько раз меньше начальной скорости пули, во сколько раз пуля легче оружия. Энергия отдачи у ручного стрелкового оружия обычно не превышает 2 кг/м и воспринимается стрелком безболезненно.
Сила отдачи и сила сопротивления отдаче (упор приклада) расположены не на одной прямой: они направлены в противоположные стороны и образуют пару сил, под воздействием которой дульная часть ствола оружия отклоняется кверху. Величина отклонения дульной части ствола данного оружия тем больше, чем больше плечо этой пары сил. Кроме того, при выстреле ствол оружия вибрирует, то есть совершает колебательные движения. В результате вибрации, дульная часть ствола в момент вылета пули может также отклоняться от первоначального положения в любую сторону (вверх, вниз, влево, вправо).
Следует всегда помнить о том, что величина этого отклонения увеличивается при неправильном использовании упора для стрельбы, загрязнения оружия, использования нестандартных патронов.
Сочетание влияния вибрации ствола, отдачи оружия и других причин приводят к образованию угла между направлением оси канала ствола до выстрела и ее направлением в момент вылета пули из канала ствола: этот угол называется углом вылета.
Угол вылета считается положительным, если ось канала ствола в момент вылета пули выше ее положения до выстрела, отрицательным — когда ниже. Влияние угла вылета на стрельбу устраняется при приведении его к нормальному бою. Но при нарушении правил ухода за оружием и его сбережением, правил прикладки оружия, использовании упора, изменяется величина угла вылета и бой оружия. С целью уменьшения вредного влияния отдачи на результаты стрельбы, применяются компенсаторы отдачи, находящиеся на дульной части ствола оружия либо съемные, крепящиеся на него.
Внешняя баллистика
Внешняя баллистика изучает процессы и явления сопровождающие движение пули, возникающие после того, как на нее прекращается воздействие пороховых газов. Основной задачей этой поддисциплины является изучение закономерностей полета пули и изучение свойств траектории ее полета.
Также, эта дисциплина дает данные для выработки правил стрельбы, составления таблиц стрельбы и расчета шкал прицелов оружия. Выводы из внешней баллистики издавна широко используются в бою при выборе прицела и точки прицеливания в зависимости от дальности стрельбы, скорости и направления ветра, температуры воздуха и других условий стрельбы.
Траектория полета пули
Траектория полета пули — это кривая линия, описываемая центром тяжести пули в процессе полета.
Траектория полета пули, полет пули в пространстве
При полете в пространстве, на пулю воздействуют две силы: сила тяжести и сила сопротивления воздуха.
Сила тяжести заставляет пулю постепенно горизонтально снижаться по направлению к плоскости земли, а сила сопротивления воздуха перманентно (непрерывно) замедляет полет пули и стремится опрокинуть ее: как результат — скорость полета пули постепенно уменьшается, а ее траектория представляет собой по форме неравномерно изогнутую кривую линию.
Сопротивление воздуха полету пули вызывается тем, что воздух представляет собой упругую среду и потому на движение в этой среде затрачивается некоторая часть энергии пули.
Сила сопротивления воздуха вызывается тремя основными факторами:
- трением воздуха
- завихрениями
- баллистической волной
Форма, свойства и типы траектории
Форма траектории зависит от величины угла возвышения. С увеличением угла возвышения, высота траектории и полная горизонтальная дальность полета пули увеличиваются, но это происходит до определенного предела, по достижении которого высота траектории продолжает увеличиваться, а полная горизонтальная дальность начинает уменьшаться.
Угол возвышения, при котором полная горизонтальная дальность полета пули становится наибольшей, называется углом наибольшей дальности. Величина угла наибольшей дальности для пуль различных видов оружия составляет около 35°.
Типы траектории полета пули
Навесная траектория — это траектория, получаемая при углах возвышения больших угла наибольшей дальности.
Настильная траектория — траектория, получаемая при углах возвышения меньших угла наибольшей дальности.
Сопряженная траектория — траектория, имеющая одинаковую горизонтальную дальность при разных углах возвышения.
При стрельбе из оружия одной и той же модели (при одинаковых начальных скоростях пули), можно получить две траектории полета с одинаковой горизонтальной дальностью: навесную и настильную.
При стрельбе из стрелкового оружия используются только настильные траектории. Чем настильнее траектория, тем на большей дистанции может быть поражена цель с одной установкой прицела и тем меньшее влияние на результаты стрельбы оказывают ошибка в определении установки прицела: в этом заключается практическое значение траектории.
Чем настильнее траектория, тем на большей дистанции может быть поражена цель с одной установкой прицела и тем меньшее влияние на результаты стрельбы оказывают ошибка в определении установки прицела: в этом заключается практическое значение траектории.
Настильность траектории характеризуется наибольшим ее превышением над линией прицеливания. При данной дальности траектория тем более настильная, чем меньше она поднимается над линией прицеливания. Кроме того, о настильности траектории можно судить по величине угла падения: траектория тем более настильна, чем меньше угол падения.
Настильность траектории влияет на величину дальности прямого выстрела, поражаемого, прикрытого и мертвого пространства.
Элементы траектории полета пули
Элементы траектории полета пули
Точка вылета — центр дульного среза ствола оружия. Точка вылета является началом траектории.
Горизонт оружия — горизонтальная плоскость, проходящая через точку вылета.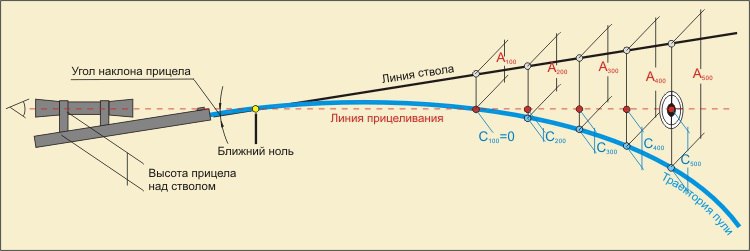
Линия возвышения — прямая линия, которая является продолжением оси канала ствола наведенного оружия.
Плоскость стрельбы — вертикальная плоскость, проходящая через линию возвышения.
Угол возвышения — угол, заключенный между линией возвышения и горизонтом оружия. Если этот угол отрицательный, то он называется углом склонения (снижения).
Линия бросания — прямая линия, являющаяся продолжением оси канала ствола в момент вылета пули.
Угол бросания — угол, заключенный между линией возвышения и линией бросания.
Угол вылета — угол, заключенный между линией возвышения и линией бросания.
Точка падения — точка пересечения траектории с горизонтом оружия.
Угол падения — угол, заключенный между касательной к траектории в точке падения и горизонтом оружия.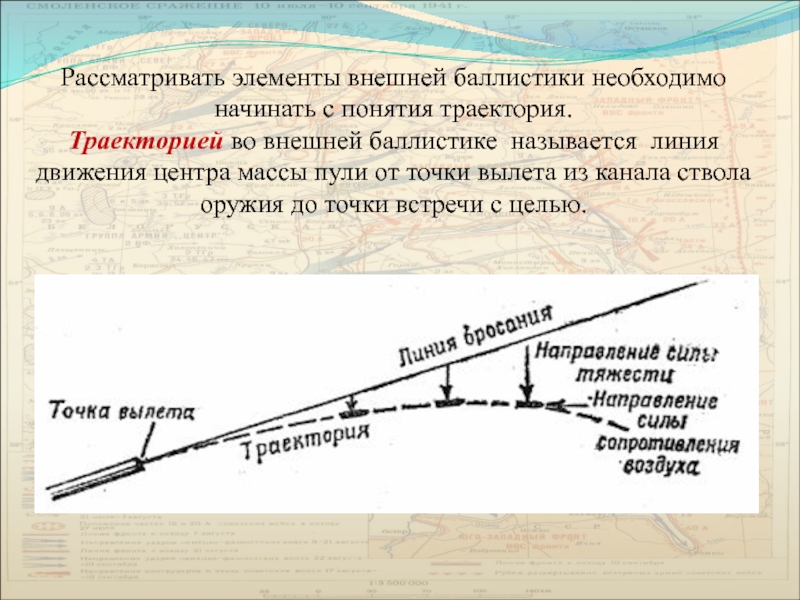
Полная горизонтальная дальность — расстояние от точки вылета до точки падения.
Окончательная скорость — скорость пули в точке падения.
Полное время полета — время движения пули от точки вылета до точки падения.
Вершина траектории — наивысшая точка траектории над горизонтом оружия.
Высота траектории — кратчайшее расстояние от вершины траектории до горизонта оружия.
Восходящая ветвь траектории — часть траектории от точки вылета до вершины.
Нисходящая ветвь траектории — часть траектории от вершины до точки падения.
Точка прицеливания (точка наводки) — точка на цели (вне ее), в которую наводится оружие.
Линия прицеливания — прямая линия, проходящая от глаза стрелка через середину прорези прицела на уровне с ее краями и вершины мушки в точку прицеливания.
Угол прицеливания — угол, заключенный между линией возвышения и линией прицеливания.
Угол места цели — угол, заключенный между линией прицеливания и горизонтом оружия. Этот угол считается положительным (+), когда цель выше, и отрицательным (-), когда цель ниже горизонта оружия.
Прицельная дальность — расстояние от точки вылета до пересечения траектории с линией прицеливания. Превышение траектории над линией прицеливания — кратчайшее расстояние от любой точки траектории до линии прицеливания.
Линия цели — прямая, соединяющая точку вылета с целью.
Наклонная дальность — расстояние от точки вылета до цели по линии цели.
Точка встречи — точка пересечения траектории с поверхностью цели (земли, преграды).
Угол встречи — угол, заключенный между касательной к траектории и касательной к поверхности цели (земли, преграды) в точке встречи. За угол встречи принимается меньший из смежных углов, измеряемый от 0 до 90°.
За угол встречи принимается меньший из смежных углов, измеряемый от 0 до 90°.
Прямой выстрел, прикрытое пространство, поражаемое пространство, мертвое пространство
Прямой выстрел
Прямой выстрел — это выстрел, при котором траектория не поднимается над линией прицеливания выше цели на всем своем протяжении.
Дальность прямого выстрела зависит от двух факторов: высоты цели и настильности траектории. Чем выше цель и чем настильнее траектория, тем больше дальность прямого выстрела и тем на большем протяжении местности цель может быть поражена с одной установкой прицела.
Также, дальность прямого выстрела может определяться по стрелковым таблицам путем сравнения высоты цели с величинами наибольшего превышения траектории над линией прицеливания или с высотой траектории.
В пределах дальности прямого выстрела, в напряженные моменты боя, стрельба может вестись без перестановки значений прицела, при этом точка прицеливания по высоте, как правило, выбирается на нижнем краю цели.
Прямой снайперский выстрел в городских условиях
Прямой снайперский выстрел в городских условиях
Практическое применение
Высота установки оптических прицелов над каналом ствола оружия в среднем составляет 7 см. На дистанции 200 метров и прицеле «2» наибольшие превышения траектории, 5 см на дистанции 100 метров и 4 см — на 150 метров практически совпадают с линией прицеливания — оптической осью оптического прицела. Высота линии прицеливания на середине дистанции 200 метров составляет 3,5 см. Происходит практическое совпадение траектории пули и линии прицеливания. Разницей в 1,5 см можно пренебречь. На дистанции 150 метров высота траектории 4 см, а высота оптической оси прицела над горизонтом оружия составляет 17-18 мм; разница по высоте составляет 3 см, что также не играет практической роли.
На дистанции 80 метров от стрелка высота траектории пули будет 3 см, а высота прицельной линии — 5 см, та же самая разница в 2 см не имеет решающего значения. Пуля ляжет всего на 2 см ниже точки прицеливания.
Пуля ляжет всего на 2 см ниже точки прицеливания.
Вертикальный разброс пуль в 2 см настолько мал, что он принципиального значения не имеет. Поэтому, стреляя с делением «2» оптического прицела, начиная с 80 метров дистанции и до 200 метров, цельтесь противнику в переносицу — вы туда и попадете ±2/3 см выше ниже на всей этой дистанции.
На дистанции 200 метров пуля попадет строго в точку прицеливания. И даже далее, на дистанции до 250 метров, цельтесь с тем же прицелом «2» противнику в «макушку», в верхний срез шапки — пуля после 200 метров дистанции резко понижается. На 250 метров, целясь таким образом, вы попадете ниже на 11 см — в лоб или переносицу.
Вышеописанный способ ведения огня может пригодиться в уличных боях, когда относительно открытые для обзора расстояния в городе составляют примерно 150-250 метров.
Поражаемое пространство
Поражаемое пространство — это расстояние на местности, на протяжении которого нисходящая ветвь траектории не превышает высоты цели.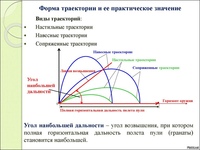
При стрельбе по целям, находящимся на расстоянии большем дальности прямого выстрела, траектория вблизи ее вершины поднимается выше цели и цель на каком-то участке не будет поражаться при той же установке прицела. Однако около цели будет такое пространство (расстояние), на котором траектория не поднимается выше цели и цель будет поражаться ею.
Глубина поражаемого пространства зависит от:
- высоты цели (чем больше высота, тем большее значение)
- настильности траектории (чем настильнее траектория, тем большее значение)
- угла наклона местности (на переднем скате она уменьшается, на обратном скате — увеличивается)
Глубину поражаемого пространства можно определить по таблицам превышения траектории над линией прицеливания путем сравнения превышения нисходящей ветви траектории на соответствующую дальность стрельбы с высотой цели, а в том случае, если высота цели меньше 1/3 высоты траектории — то по форме тысячной.
Для увеличения глубины поражаемого пространства на наклонной местности огневую позицию нужно выбирать так, чтобы местность в расположении противника по возможности совпадала с линией прицеливания.
Прикрытое, поражаемое и мертвое пространство
Прикрытое пространство — это пространство за укрытием не пробиваемым пулей, от его гребня и до точки встречи.
Прикрытое, мертвое и поражаемое пространство
Чем больше высота укрытия и чем настильнее траектория — тем больше прикрытое пространство. Глубину прикрытого пространства можно определить по таблицам превышения траектории над линией прицеливания: путем подбора отыскивается превышение, соответствующее высоте укрытия и дальности до него. После нахождения превышения определяется соответствующая ему установка прицела и дальность стрельбы.
Разность между определенной дальностью стрельбы и дальностью до укрытия представляет собой величину глубины прикрытого пространства.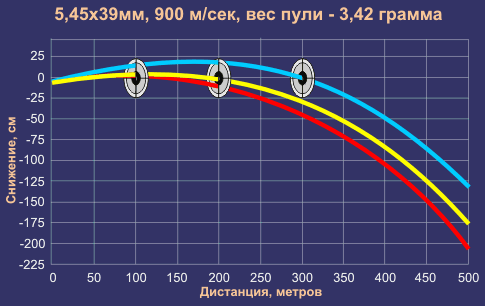
Мертвое пространство — это часть прикрытого пространства, на котором цель не может быть поражена при данной траектории.
Чем больше высота укрытия, меньше высота цели и настильнее траектория — тем больше мертвое пространство.
Поражаемое пространство — это часть прикрытого пространства, на которой цель может быть поражена. Глубина мертвого пространства равна разности прикрытого и поражаемого пространства.
Знание величины поражаемого пространства, прикрытого пространства, мертвого пространства позволяет правильно использовать укрытия для защиты от огня противника, а также принимать меры для уменьшения мертвых пространств путем правильного выбора огневых позиций и обстрела целей из оружия с более навесной траекторией.
Деривация
Деривация
Это достаточно сложный процесс. Вследствие одновременного воздействия на пулю вращательного движения, придающего ей устойчивое положение в полете и сопротивления воздуха, стремящегося опрокинуть пулю головной частью назад, ось пули отклоняется от направления полета в сторону вращения.
В результате этого, пуля встречает большее сопротивление воздуха одной из своих сторон, а поэтому отклоняется от плоскости стрельбы все больше и больше в сторону вращения. Такое отклонение вращающейся пули в сторону от плоскости стрельбы называется деривацией.
Деривация возрастает непропорционально расстоянию полета пули, вследствие чего последняя отклоняется все больше и больше в сторону от намеченной цели и ее траектория представляет собой кривую линию. Направление отклонения пули зависит от направления нарезов ствола оружия: при левосторонней нарезке ствола деривация уводит пулю в левую сторону, при правосторонней — в правую.
На дистанциях стрельбы до 300 метров включительно, деривация не имеет практического значения.
| Дистанция, м | Деривация, см | Тысячные (горизонтальная поправка прицела) | Точка прицеливания без поправок (винтовка СВД) |
| 100 | 0 | 0 | центр прицела |
| 200 | 1 | 0 | то же |
| 300 | 2 | 0,1 | то же |
| 400 | 4 | 0,1 | левый (от стрелка) глаз противника |
| 500 | 7 | 0,1 | в левую сторону головы между глазом и ухом |
| 600 | 12 | 0,2 | левый обрез головы противника |
| 700 | 19 | 0,2 | над центром погона на плече противника |
| 800 | 29 | 0,3 | без поправок точная стрельба не производится |
| 900 | 43 | 0,5 | то же |
| 1000 | 62 | 0,6 | то же |
Читать другие материалы раздела «Подготовка снайпера»
Вопросы внешней баллистики рассмотрим на примере пулевого выстрела, так как при полной тождественности всех понятий и определений для дробового заряда и пули так проще объяснить образование траектории.
Если представить, что на пулю, покинувшую канал ствола, действует только сила тяжести, то, как всякое свободно падающее тело, она будет падать — по закону свободного падения — за первую секунду на 4,9 м, задве -на 19,6 м, за три-на 44,1 м, за четыре-на 78,4 ми за пять секунд-на 122,5 м (рис.
Тогда, если бы пуля двигалась в безвоздушном пространстве по инерции и на нее действовала бы сила тяжести, то относительно направления оси канала ствола она опускалась бы вниз за каждую секунду на указанное расстояние и не попала бы в цель. Следовательно, для меткого попадания надо направлять Рис. 10. Траектория пули в безвоздушном пространстве Как видно из рисунка, кривая абсолютно симметрична относительно вершины траектории, угол бросания и угол падения равны.
Рис. 11. Окончательная скорость легкой и тяжелой пуль при стрельбе из 7,62-мм служебной винтовки
пожие материалы |
Тема: Основы и правила стрельбы. Явление выстрела. Траектория полёта пули и её элементов. Прямой выстрел, поражаемое | Планы конспекты 10 класс по НВП
Тема: Основы и правила стрельбы. Явление выстрела. Траектория полёта пули и её элементов. Прямой выстрел, поражаемое
08. 06.2013 29296 0
06.2013 29296 0 УТВЕРЖДАЮ
Директор школы: ______________
«__» _____________ 200_ г.
План — конспект
проведения урока по начальной военной подготовке по разделу
ОГНЕВАЯ ПОДГОТОВКА с учащимися 10 класса
Тема: Основы и правила стрельбы. Явление выстрела. Траектория полёта
пули и её элементов. Прямой выстрел, поражаемое и мертвое
пространство и их практическое значение.
Учебная цель: Ознакомить учащихся с основами и правилами
стрельбы, рассказать о явлении выстрела.
Воспитательная цель: Воспитать у учащихся дисциплинированность, ответственность при обращении с оружием и боеприпасами.
Время. _____
Метод. Рассказ.
Место проведения занятий. Кабинет НВП.
Руководство и пособия. Наставление по стрелковому оружию. Учебник по НВП.
Учебные вопросы.
1. Явление выстрела.
2. Траектория полёта пули и её элементов.
3. Прямой выстрел, поражаемое и мертвое пространство, и их практическое значение.
Вводная часть 15 мин.
А) Построение взвода и проверка внешнего вида 5 мин.
Б) Проверка домашнего задания 10 мин.
Основная часть 30 мин.
Вступление 5 мин.
1. Чтобы хорошо стрелять, надо не только знать устройство оружия, но и приёмы стрельбы, и их правила.
Изложение
основного материала 20 мин.
1. Выстрелом называется выбрасывание пули из канала ствола оружия под давлением газов, образующихся при сгорании порохового заряда. Выстрел происходит в очень короткий промежуток времени (0, 001 – 0, 06 секунд). От удара по капсюлю патрона образуется пламя, которое воспламеняет пороховой заряд. При сгорании порохового заряда образуется большое количество сильно нагретых газов, которые в канале ствола создают высокое давление, действующее во все стороны с одинаковой силой. Под давлением газов пуля сдвигается с места, врезается в нарезы, продвигается по каналу ствола с непрерывно возрастающей скоростью и выбрасывает наружу по направлению оси канала ствола. Раскаленные газы, истекающие из канала ствола вслед за пулей, при встрече с воздухом образуется пламя и ударная волна, которая, является источником звука при выстреле.
Поскольку нарезы в стенках ствола выполнены винтообразно, пуля, продвигаясь по каналу ствола, получает вращательное движение.
В выстреле различают 4 периода.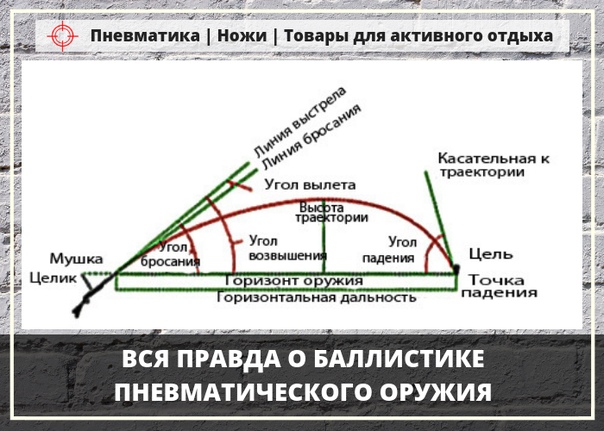
Предварительный период длится от начала горения порохового заряда до врезания оболочки пули в нарезы. В этот период в канале ствола создаётся давление 2500 – 5000 Н/ см.3 (250 – 500 кгс/см2), которое необходимо для того, чтобы сдвинуть пулю с места и преодолеть сопротивление её оболочки врезанию в нарезы.
Первый, или основной, период длится от начала движения пули до полного сгорания порохового заряда. При прохождении пули 4 – 6 см., количество газов растёт быстрее, давление газов быстро повышается и достигает наибольшей величины (2800 кгс/см.2).
Второй период длится от момента полного сгорания порохового заряда до момента выстрела пули из канала ствола. Сильно сжатые и нагретые газы расширяются, давят на пулю и увеличивают её скорость движения.
Третий период, длится от момента вылета пули из канала ствола до момента прекращения возрастания скорости движения пули.
2.
Начальная скорость движения пули называется та скорость, с которой пуля
покидает канал ствола. Она измеряется м/с. Начальная скорость движения пули
является одной из важных характеристик боевых свойств оружия. Величина
начальной скорости пули зависит от длины ствола, массы пули, массы порохового
заряда. Чем длиннее ствол (до известных пределов), тем дольше действует на пулю
пороховые газы и тем больше её начальная скорость движения.
Она измеряется м/с. Начальная скорость движения пули
является одной из важных характеристик боевых свойств оружия. Величина
начальной скорости пули зависит от длины ствола, массы пули, массы порохового
заряда. Чем длиннее ствол (до известных пределов), тем дольше действует на пулю
пороховые газы и тем больше её начальная скорость движения.
3. Давление газов в канале ствола действует во все стороны с одинаковой силой, при выстреле оно не только выталкивает пулю вперёд, но и отталкивает оружие назад. движение оружия назад во время выстрела называется отдачей. В результате отдачи пуля вылетает из канала ствола не в том направлении оси, которое было придано её до выстрела, а в направлении, которое занимает ось канала ствола в момент вылета из него пули. Угол, образуемый после выстрела называется углом вылета пули. Для того чтобы максимально сохранить постоянную величину угла вылета, стрелок должен одинаково выполнять все элементы изготовки.
2. Полёт пули в воздухе
начинается по прямой линии.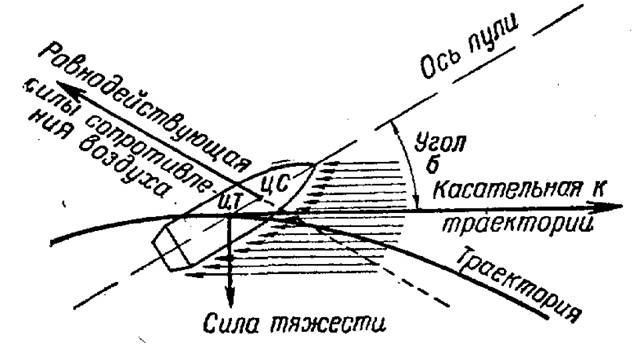 Эта линия называется линией бросания. При полёте в
воздухе на пулю действует две силы: сила тяжести и сила сопротивления воздуха.
Сила тяжести отталкивает пулю от линии бросания, а сила сопротивления замедляет
движение пули в воздухе. Под действием
двух сил пуля летит по кривой, расположенной ниже уровня бросания. Кривая линия
, которую описывает центр тяжести пули при полёте в воздухе, называется –
траекторией.
Эта линия называется линией бросания. При полёте в
воздухе на пулю действует две силы: сила тяжести и сила сопротивления воздуха.
Сила тяжести отталкивает пулю от линии бросания, а сила сопротивления замедляет
движение пули в воздухе. Под действием
двух сил пуля летит по кривой, расположенной ниже уровня бросания. Кривая линия
, которую описывает центр тяжести пули при полёте в воздухе, называется –
траекторией.
3. Прямым выстрелом называется выстрел, при котором траектория полёта пули не поднимается над линией прицеливания выше цели на всём своём протяжении.
Дальность полёта пули зависит от высоты цели. Чем выше цель, тем больше дальность прямого выстрела.
Заключительная часть 5 мин.
1. Напомнить тему, цели урока и как они достигнуты.
2. Выделить лучшие ответы и недостатки по контрольному опросу
3. Объявить раздел и тему следующего занятия, а также форму одежды.
4. Задание на дом. 1. Явление выстрела. 2. Траектория полёта пули и её элементов.
Траектория полёта пули и её элементов.
3. Прямой выстрел, поражаемое и мертвое пространство, и их практическое значение.
Преподаватель-организатор НВП: _____________________________
Как работают пули в видеоиграх? / Хабр
Игры FPS (first-person shooter, шутер от первого лица) стали неотъемлемой частью видеоигровой индустрии ещё с момента появления в 1992 году популярнейшей
Wolfenstein 3D. С тех пор жанр эволюционировал: улучшалась графика, увеличивались бюджеты на разработку, развивалась экосистема киберспорта. Но что насчёт их фундамента — механики стрельбы? Как проходило развитие на этом фронте? Почему в некоторых играх оружие кажется реальными, а в других похоже на игрушки?
В предыдущую эпоху многие игры для рендеринга 3D-сцен в 2D-изображения использовали технику под названием
raycasting («бросание лучей»). Raycasting позволяет движку определять первый объект, с которым пересечётся луч. Но потом разработчики задались вопросом: «Что, если выпустить луч из ствола оружия, чтобы имитировать пулю?» Благодаря этой идее родился hitscan («сканирование попадания»).
Но потом разработчики задались вопросом: «Что, если выпустить луч из ствола оружия, чтобы имитировать пулю?» Благодаря этой идее родился hitscan («сканирование попадания»).
Пример raycasting
В большинстве реализаций оружия с hitscan при выстреле игрока физический движок выполняет следующие операции:
- Определяет направление, в котором указывает оружие.
- Выпускает из ствола оружия луч на заданное расстояние.
- Использует raycasting для определения того, попал ли луч в объект.
Если движок определил, что объект находится на линии огня, то он сообщит ему об этом, сказав, что в него «попала» пуля. Затем цель может выполнить все вычисления, необходимые для регистрации повреждений.
Из Unity. Точка A обозначает оружие, испускающее луч до максимальной точки B. Луч сталкивается с кубом, которому движок сообщает, что в него попали.
Hitscan по своей природе прост, но для добавления другой логики можно внести множество различных модификаций:
- Если мы продолжим луч за первый объект, в который он попал, то сможем пронзать несколько объектов на линии, как рельсовая пушка (railgun) в Quake
- Если убрать у луча максимальную дальность, то мы получим лазер, который будет лететь вечно, пока во что-то не попадёт
- Можно программно сделать некоторые поверхности отражающими, чтобы от них отскакивали пули
 Способность персонажа Гэндзи deflect — пример отражающей поверхности.
Способность персонажа Гэндзи deflect — пример отражающей поверхности.Основное преимущество raycasting в его огромной скорости обработки. Он быстро вычисляется и не требует дополнительной памяти или процессорного времени на создание нового физического объекта. Это значит, что сетевой код, необходимый для синхронизации множества клиентов, будет минимальным, потому что серверу нужно только отслеживать направление луча. Отдача тоже реализуется просто, для имитации этого эффекта достаточно добавить небольшое отклонение в прицеле оружия.
Поэтому неудивительно, что в логике стрельбы многих игр используется hitscan. Классическими примерами являются Wolfenstein 3D и Doom, но эта технология используется и в современных играх. Такие персонажи, как Солдат 76, Маккри и Роковая вдова из Overwatch используют оружие с hitscan, а большинство оружия в Call of Duty тоже основано на hitscan.
Overwatch, Call of Duty, Wolfenstein 3D
Так почему же такой подход не используется во всех играх?
Во-первых, как вы наверно заметили, лучи имеют бесконечно высокую скорость перемещения, то есть мгновенно попадают в конечную точку. Между выстрелом пулей и попаданием в объект нет времени движения пули. Это значит, что если луч попал в объект, от пули уклониться невозможно, даже если цель находится в нескольких километрах от игрока.
Между выстрелом пулей и попаданием в объект нет времени движения пули. Это значит, что если луч попал в объект, от пули уклониться невозможно, даже если цель находится в нескольких километрах от игрока.
Halo. Заметьте, что дульная вспышка и эффекты попадания по земле происходят одновременно.
Во-вторых, в большинстве реализаций hitscan используются прямые лучи. Это значит, что сложно учесть ветер, гравитацию и другие внешние факторы, которые могут влиять на пулю после вылетания из ствола. Программисты могут добавлять всякие хитрости, чтобы луч имитировал настоящие пули, но как только игрок «выстрелил» лучом, нет никакой возможности изменить его путь посередине.
Во многих «казуальных» играх всё равно используется hitscan, потому что он упрощает кривую обучения для большинства игроков-новичков. Но как насчёт игр, стремящихся передать «реальные» ощущения от стрельбы? При таких ограничениях этого добиться невозможно, поэтому необходим другой метод.
Этот термин может показаться сложным, но на абстрактном уровне идея довольно проста. Каждая выстреливаемая из оружия пуля или снаряд создаёт в сцене новый физический объект. Он обладает собственной массой, скоростью и ограничивающим параллелепипедом контакта (hitbox), которые отслеживаются движком игры.
Каждая выстреливаемая из оружия пуля или снаряд создаёт в сцене новый физический объект. Он обладает собственной массой, скоростью и ограничивающим параллелепипедом контакта (hitbox), которые отслеживаются движком игры.
Max Payne 3
Преимущества баллистики в полной мере проявляются в играх, в которых реализм имеет наивысший приоритет. Так как каждый летящий объект существует сам по себе, мы можем учесть влияние на него ветра, трения, гравитации, температуры — любой силы, которая должна действовать на пулю. Теперь, когда мы способны менять физику, игрокам можно пользоваться более разнообразным вооружением, а не только простыми пистолетами и лазерами; мы можем добавить в свой арсенал гранаты и ракеты.
Так как пули в такой системе не движутся со скоростью света, можно также реализовать и временны́е свойства:
- «Буллет-тайм», применяемый в Max Payne, Sniper Elite и Superhot.
- Время перемещения пуль, то есть при стрельбе на дальние расстояния (или стрельбе медленно двигающимся снарядом) критически важным становится упреждение.

- Отложенные взрывы снарядов, например гранат
Из-за этих дополнительных вычислений обработка становится более затратной, чем при использовании hitscan. Для обеспечения синхронизации серверам приходится выполнять намного больше работы, необходимо устранять расхождения или конфликты в логике на стороне клиентов, чтобы все игроки в пределах одного сервера находились в одинаковых условиях.
Superhot, Battlefield 1, Overwatch
Существует множество обходных путей для максимального повышения производительности. Например, движок может хранить пул объектов, загруженных до начала игры и «включать» их по мере необходимости. После попадания в поверхность можно воспроизвести анимацию баллистики и отключить пулю, сохранив её на будущее. Этот способ позволяет экономить вычислительные ресурсы и память, занимаемые многократным созданием и уничтожением объектов.
Также существует множество способов выполнения вычислений, но на высоком уровне разница заключается в том, где они решают обрабатывать «такт» игры — единицу измерения времени:
- Такт вычисляется отдельно от логики рендеринга, то есть игра будет иметь более точное воспроизведение объектов даже при пропуске кадров.
 Для вычисления точного времени, прошедшего с момента предыдущего рендеринга, требуется больше логики.
Для вычисления точного времени, прошедшего с момента предыдущего рендеринга, требуется больше логики. - Вычисление такта в каждом кадре; привязка физики к частоте кадров. Если отключить ограничение на максимальную частоту кадров или если игра начнёт пропускать кадры, то физика мира ускорится или будет тормозить.
Последствия привязки движения к тактам чётко заметны, когда снаряды движутся достаточно быстро, чтобы перемещаться между тактами на довольно большое расстояние. Могут возникать ситуации, когда объекты «проходят» сквозь друг друга, потому что в движке они никогда не пересекались.
Всё это кажется сложным, поэтому многие люди думают, что это относительно новый метод; однако на самом деле он возник раньше, чем hitscan! До игр жанра FPS существовало множество шутеров с видом сверху, например Asteroids, Space Invaders или Galaxian. Это аркадные игры 70-х годов, в которых уже была реализована баллистика снарядов, хотя и довольно примитивно.
Asteroids. Снаряды довольно сложно увидеть, но они есть!
Но даже со всеми этими функциями мы не может воссоздать реалистичную модель реального мира. Можно ли как-то воспользоваться преимуществами обоих методов?
Большинство игровых движков способно обрабатывать оба типа симуляций пуль: hitscan и баллистику. Это позволяет реализовать огромный выбор оружия; в таких играх, как
Halo,
GTAи
Half-Lifeесть оружие, которое может поддерживать оба типа физики.
Halo. В Assault Rifle используется hitscan; в Needler используется баллистика снарядов
Разработчики также могут смешивать обе техники, чтобы закрывать слабые места каждой из систем и обеспечивать более реалистичное поведение. Например, для устранения проблемы прохождения объектов сквозь друг друга каждая пуля в каждом такте движка может испускать луч. Это позволяет движку увидеть, пересекутся ли какие-то из лучей между тактами, сталкиваясь в воздухе.![]()
Также их можно объединять для улучшения особенностей игры. Отличным примером подобного является серия Sniper Elite; после нажатия на спусковой крючок движок использует hitscan, чтобы определить, сделан ли выстрел достаточно близко к любому обнаруживаемому объекту для включения slow motion. Если да, то выстрел пулей производится с расчётом баллистики в режиме «буллет-тайм».
Sniper Elite
Итак, мы рассмотрели основы поведения пуль в видеоиграх! Интересно, что улучшения в этой области в основном заключаются в небольших оптимизациях и усовершенствованиях, а не в масштабной переработке. После выпуска нескольких первых революционных игр мы не сделали никаких значительных шагов и прорывов.
Что же дальше? Как будет развиваться эта область в дальнейшем?
Я не думаю, что в ближайшее время гибридный подход исчезнет, ведь он обеспечивает дополнительные преимущества. Но я прогнозирую, что со стороны баллистики снарядов произойдёт множество улучшений.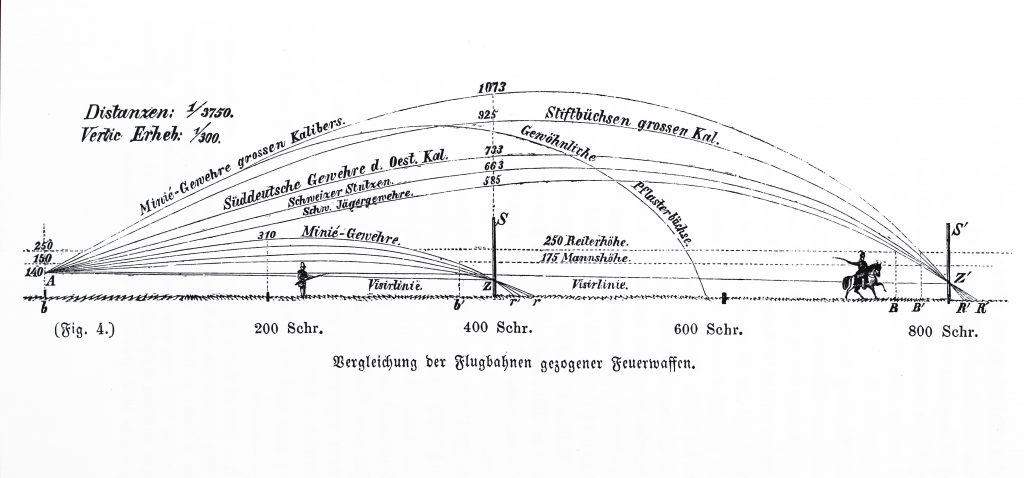 Частота вычисления тактов продолжает увеличиваться (ведь мощь ЦП растёт), и мы сможем приблизиться к асимптотическому пределу симуляции пули «реального мира».
Частота вычисления тактов продолжает увеличиваться (ведь мощь ЦП растёт), и мы сможем приблизиться к асимптотическому пределу симуляции пули «реального мира».
Внешняя баллистика — Hornady Manufacturing, Inc
От ствола к мишени
Внешняя баллистика касается характеристик пуль Hornady с момента их выхода из ствола до момента попадания в цель. Мы не занимаемся ни внутренней баллистикой, областью инженера-оружейника или химика-пороха, ни конечной баллистикой, областью судебного патологоанатома или других научных специалистов.
Терминальная баллистика очень важна для военных, полиции и охотников.Хотя нет никакого способа смоделировать конечное поведение всех снарядов во всех средах при всех скоростях, мы кратко коснемся этого предмета в разделе, озаглавленном «Энергия». Сейчас мы сосредоточимся на внешней баллистике.
Траектория — это описание траектории полета снаряда относительно некоторых известных и фиксированных точек. Траектории ВВ, снарядов полевой артиллерии, морских орудий, минометных снарядов и пуль стрелкового оружия имеют параболическую форму. В стволе или миномете движение снаряда направлено и полностью определяется давлением газов позади него.Но как только снаряд вылетает из ствола, на его полет начинают влиять две другие силы. Во-первых, сопротивление воздуха. Второе — гравитация. Каким бы ни был угол вылета и начальная скорость снаряда или пули, снаряд или пуля будут терять скорость из-за сопротивления воздуха и терять высоту из-за силы тяжести. Результатом является параболическая форма траектории.
В стволе или миномете движение снаряда направлено и полностью определяется давлением газов позади него.Но как только снаряд вылетает из ствола, на его полет начинают влиять две другие силы. Во-первых, сопротивление воздуха. Второе — гравитация. Каким бы ни был угол вылета и начальная скорость снаряда или пули, снаряд или пуля будут терять скорость из-за сопротивления воздуха и терять высоту из-за силы тяжести. Результатом является параболическая форма траектории.
Ограничив наше обсуждение только пулями, мы можем привести иллюстрации параболической кривой траектории и связанных с ней понятий.На рисунке A (увеличенном для наглядности) мы показываем дуло (слева) и цель (справа), предполагаемые горизонтальными на одной и той же базовой линии (для практических целей базовая линия эквивалентна линии визирования). Ствол огнестрельного оружия приподнят. Ось канала ствола становится линией вылета пули из дульного среза. Гравитация и сопротивление воздуха вступают в игру настолько быстро, что линия вылета пули касается траектории только у дульного среза.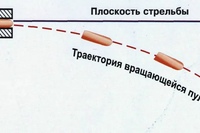
Рисунок А
Траектория сразу начинает опускаться ниже оси ствола.Угол вылета (у стрелкового оружия вообще очень небольшой) образуется пересечением линии вылета и базовой линии. Средняя траектория — это высота пули над базовой линией на полпути между дульным срезом и точкой попадания (здесь — целью).
На рис. B для сравнения двух разных траекторий используются одинаковые огнестрельное оружие, пуля и начальная скорость (ствол для простоты представлен только в одном положении). Разница между траекториями возникает из-за разных углов отхода, необходимых для пристрелки огнестрельного оружия (изменения точки попадания) на двух дистанциях; 100 ярдов и 200 ярдов.Траектории падают ниже базовой линии (линии прямой видимости) на рис. B при нулевых значениях 100 и 200 ярдов соответственно. Траектории пули за пределами точки попадания описываются в дюймах падения.
Хотя имеет смысл рассчитывать траектории морских снарядов в терминах углов вылета, и хотя это можно сделать и для траекторий стрелкового оружия, основным ориентиром стрелка в поле зрения является линия прицеливания.
Рисунок В
Баллистический коэффициент
Прежде чем обсуждать эту тему более подробно, давайте развеем некоторые мифы, окружающие ее.Что бы вы ни слышали раньше, это факты:
- Абсолютного и неизменного баллистического коэффициента (БК) не существует
- Баллистические коэффициенты являются лишь одним из факторов при выборе пули для различных видов стрельбы.
- Баллистический коэффициент может меняться в зависимости от (1) высоты, (2) температуры, (3) атмосферного давления и (4) относительной влажности.
- Баллистические коэффициенты — это показатели относительной эффективности пули.
- Баллистические коэффициенты не являются мерой качества пули.
- Более высокие значения БК не обязательно делают пулю «лучше».
- Более низкий БК не обязательно делает пулю «хуже».
Баллистический коэффициент — это мера относительной способности пули преодолевать сопротивление воздуха. Каждой пуле можно присвоить числовое значение, выражающее эту эффективность. В основе этой величины лежит соотношение, сравнивающее ТТХ конкретной пули с известными траекторными характеристиками стандартного снаряда.Соотношение сравнивает сопротивление пули (потеря скорости из-за сопротивления воздуха, возникающего в полете) с сопротивлением стандартного снаряда. Выражается в виде формулы,
Каждой пуле можно присвоить числовое значение, выражающее эту эффективность. В основе этой величины лежит соотношение, сравнивающее ТТХ конкретной пули с известными траекторными характеристиками стандартного снаряда.Соотношение сравнивает сопротивление пули (потеря скорости из-за сопротивления воздуха, возникающего в полете) с сопротивлением стандартного снаряда. Выражается в виде формулы,
Обратите внимание, что баллистические коэффициенты в этой книге, за единственным исключением, меньше единицы [1.0], что указывает на то, что эти испытательные снаряды — пули для стрелкового оружия — встретили большее сопротивление, чем стандартные. Единственным исключением во всей линейке пуль Hornady является наша пуля 50 калибра (диаметр 0,510 дюйма) AMAX Ultra High Coefficient 750 гран.Его баллистический коэффициент равен 1,050.
Стандартным снарядом, с которым сравнивались все пули Hornady, была модель G1, основанная на работе, начатой во Франции и усовершенствованной в Лаборатории баллистических исследований армии США, Абердинский испытательный полигон, Мэриленд. Баллистические коэффициенты для всех пуль Hornady были определены с помощью компьютерных расчетов с использованием данных тестовых стрельб, проведенных на нашем 200-ярдовом подземном полигоне. Наши пули ELD-X® и ELD® Match измеряются с помощью доплеровского радара на больших расстояниях.
Баллистические коэффициенты для всех пуль Hornady были определены с помощью компьютерных расчетов с использованием данных тестовых стрельб, проведенных на нашем 200-ярдовом подземном полигоне. Наши пули ELD-X® и ELD® Match измеряются с помощью доплеровского радара на больших расстояниях.
При расчете баллистического коэффициента учитываются как коэффициенты формы, так и коэффициенты поперечной плотности. С практической точки зрения большинство стрелков понимают, что пули с заостренной формой легче сохраняют свою скорость, чем пули с круглым наконечником или пули с плоским наконечником. Это можно непосредственно наблюдать по количеству сбрасываемых пуль одинакового веса, но разной формы, выпущенных на одну и ту же дистанцию до цели. Иными словами, пули с круглым носом и заостренные пули потребуют различных настроек прицела для достижения одинакового нуля на одном и том же расстоянии.Если более обтекаемые пули лучше сохраняют свою скорость, более тяжелые обтекаемые пули той же формы будут превосходить более легкие пули при той же начальной скорости.
Следующие примеры быстро демонстрируют важность формы для сохранения скорости и плоской траектории. Мы выбрали для сравнения в этом примере две пули одинакового калибра, веса и поперечной плотности, выпущенные с одинаковой начальной скоростью 3000 футов в секунду. Форма — единственная переменная в этом примере; все остальные факторы считались постоянными.Обратите внимание на заметную разницу в поведении пули в показанных диапазонах. Пуля с круглым носом теряет начальную скорость быстрее, чем пуля со шпилем. Поскольку энергия является произведением массы на квадрат скорости, более быстрая потеря скорости пулей с круглым носом приводит к еще более быстрой потере энергии. Наиболее драматично, поскольку менее эффективная форма с круглым носом теряет свою скорость, эффекты гравитации проявляются в виде большего падения пули по сравнению с пулей со шпилем.
30 КАЛ. (.308″ ДИАМ.) 180-гранный Spire Point
Плотность сечения: 0,271
Баллистический коэффициент: 0,425
| Диапазон (ярдов) | Скорость (FPS) | Энергия (FT-LB) | 100 ярдов НОЛЬ |
| Морда | 3000 | 3597 | -1,5 дюйма |
| 50 | 2887 | 3331 | -0. |
| 100 | 2777 | 3082 | 0,0″ |
| 200 | 2565 | 2629 | -3,0″ |
| 300 | 2362 | 2230 | -11,3″ |
| 400 | 2169 | 1880 | -25,9″ |
| 500 | 1985 | 1574 | -47.8 дюймов |
30 КАЛ. (0,308 дюйма в диаметре) 180 гран с круглым носом
Плотность сечения: 0,271
Баллистический коэффициент: 0,241
| Диапазон (ярдов) | Скорость (FPS) | Энергия (фут-фунт) | 100 ярдов, ноль |
| Морда | 3000 | 3597 | -1,5 дюйма |
| 50 | 2803 | 3139 | -0.2″ |
| 100 | 2614 | 2731 | 0,0″ |
| 200 | 2259 | 2040 | -3,6 дюйма |
| 300 | 1933 | 1493 | -14,1″ |
| 400 | 1639 | 1073 | -34,0″ |
| 500 | 1385 | 767 | -67.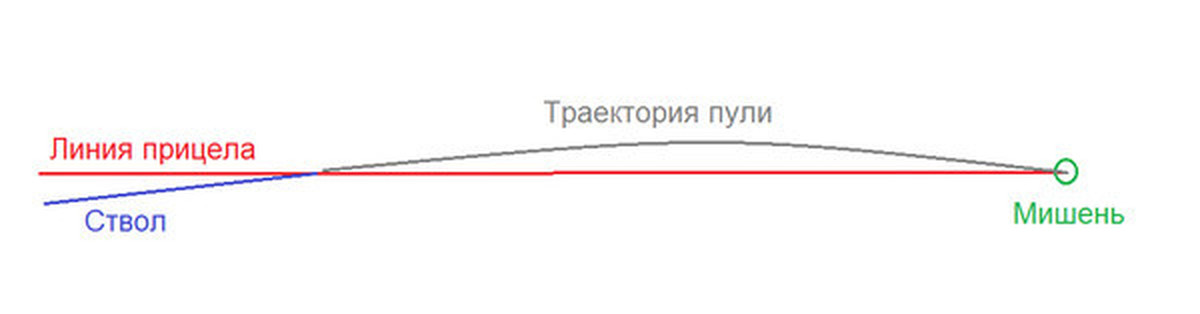 0″ 0″ |
Является ли это сравнение полностью аргументом против использования пуль с круглым наконечником? Ни в коем случае; на дистанциях от 100 до 200 ярдов, типичных для большой охоты, круглый нос не сдается. Более того, многие, кто охотится с ними, считают их совершенно надежными на предполагаемых расстояниях. Для этих людей уверенность значит больше, чем более низкий баллистический коэффициент.
Поправочные коэффициенты
Баллистические коэффициенты рассчитываются не только применительно к штатному снаряду, но и применительно к стандартным условиям испытаний.Все баллистические коэффициенты и баллистические таблицы в этой книге приведены к стандартным условиям. Это стандартные условия для Абердинского полигона.
- Высота: Уровень моря
- Температура: 59° по Фаренгейту
- Атмосферное давление: 29,53 дюйма ртутного столба
- Относительная влажность: 78%
Что происходит, когда условия нестандартны? Эти четыре тестовых примера продемонстрируют изменения расчетного баллистического коэффициента в результате поочередного изменения различных тестовых факторов.
Тест №1: стандартные условия
Высота: Уровень моря
Температура: 59°F
Барометрическое давление: 29,53″
Относительная влажность: 78%
| Диапазон (ярдов) | Скорость (FPS) | Траектория 100 ярдов Ноль |
| Морда | 2900 | -1,5 дюйма |
| 100 | 2627 | 0.0″ |
| 200 | 2371 | -3,6 дюйма |
| 300 | 2129 | -13,3″ |
| 400 | 1901 | -30,8″ |
| 500 | 1690 | -57,9″ |
Результаты: Расчетный баллистический коэффициент равен 0,338
Тест №2: более высокая температура
Высота: Уровень моря
Температура: 89°F
Барометрическое давление: 29. 53 дюйма
53 дюйма
Относительная влажность: 78%
| Диапазон (ярдов) | Скорость (FPS) | Траектория 100 ярдов Ноль |
| Морда | 2900 | -1,5 дюйма |
| 100 | 2640 | 0,0″ |
| 200 | 2395 | -3,5 дюйма |
| 300 | 2162 | -13.1″ |
| 400 | 1943 | -30,1″ |
| 500 | 1739 | -56,4″ |
Результаты: Из-за меньшей плотности воздуха (более высокие температуры) расчетная величина Б.К. составляет 0,355.
Тест №3: более высокое атмосферное давление
Высота: Уровень моря
Температура: 59°F
Барометрическое давление: 31,00″
Относительная влажность: 78%
| Диапазон (ярдов) | Скорость (FPS) | Траектория 100 ярдов Ноль |
| Морда | 2900 | -1. 5 дюймов 5 дюймов |
| 100 | 2614 | 0,0″ |
| 200 | 2346 | -3,6 дюйма |
| 300 | 2094 | -13,6″ |
| 400 | 1858 | -31,5″ |
| 500 | 1641 | -59,5″ |
Результаты: Из-за более плотного воздуха (более высокого атмосферного давления) расчетное значение B.С. составляет 0,322.
Тест №4: Большая высота
Высота: Уровень моря
Температура: 29°F
Барометрическое давление: 21,00″
Относительная влажность: 78%
| Диапазон (ярдов) | Скорость (FPS) | Траектория 100 ярдов Ноль |
| Морда | 2900 | -1,5 дюйма |
| 100 | 2693 | 0. 0″ 0″ |
| 200 | 2495 | -3,3″ |
| 300 | 2306 | -12,2″ |
| 400 | 2124 | -27,6″ |
| 500 | 1952 | -50,8″ |
Результаты: Из-за меньшей плотности воздуха (большая высота) расчетная Б.К. составляет 0,448.
.338 расчетный баллистический коэффициент варьировался от 0,322 до 0,448 в зависимости от условий. Здравый смысл подсказывает, что пуля может работать лучше при более высоких температурах (менее плотный воздух), при более низком атмосферном давлении (меньшее давление воздуха) и на больших высотах (гораздо более легкий воздух). Когда меньше воздуха, чтобы противостоять полету пули, она станет более эффективной — и наоборот. Чем можно объяснить существенно нестандартные условия подготовки, скажем, к крупной охоте? Предполагая, что вы знаете температуру, барометрическое давление и баллистический коэффициент пули, которую вы будете стрелять в нестандартных условиях, вы можете рассчитать кажущийся баллистический коэффициент пули и иначе найти траекторию для вашего места с нестандартными условиями.
Сопротивление пули во многом определяется плотностью воздуха, в котором она летит. Первым коэффициентом преобразования для корректировки изменений плотности воздуха является соотношение:
, который используется в качестве множителя при расчете коррекции. Поправочный коэффициент для температуры — другое соотношение, но с изюминкой:
.Добавление 459,4° к температуре объекта и стандартной температуре соответствует абсолютной шкале Ренкина. (Абсолютный ноль равен -459.4° по Фаренгейту или 0° по Ранкину.) Полученное соотношение также является множителем в процессе коррекции.
Коррекция относительной влажности также может быть сделана, но процесс коррекции утомителен, а полученная точность незначительна. Во всяком случае, хотя мы видели барометры в лагере и термометры на тропе, мы не можем припомнить, чтобы охотники таскали с собой гигрометры. Кроме того, мы уже уловили основные факторы, требующие корректировки.
Предположим, что мы столкнулись со следующими условиями на охоте.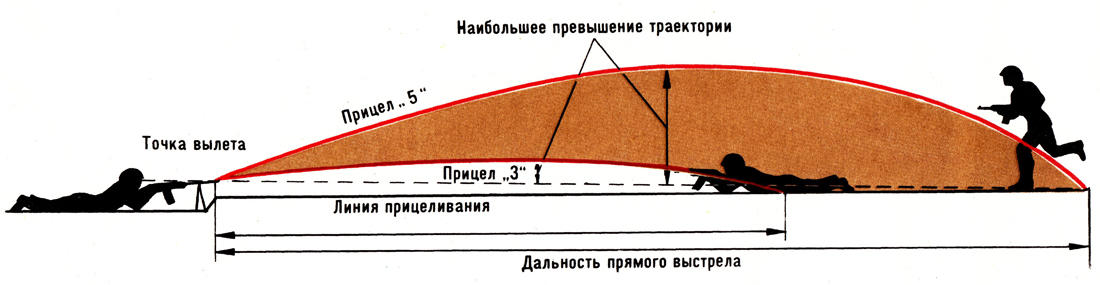 Температура холодная 29° по Фаренгейту, барометрическое давление 21,00″ ртутного столба и относительная влажность 85%. Подумайте об этом минуту, и кажется, что мы на горной охоте в очень сырых условиях. Относительная влажность очень близко до штатных 78%, так что о регулировках там не заморачиваемся.Но температура и атмосферное давление далеко не стандартные.Как они повлияют на снаряженные нами боеприпасы с баллистическим коэффициентом штатного состояния .338?
Температура холодная 29° по Фаренгейту, барометрическое давление 21,00″ ртутного столба и относительная влажность 85%. Подумайте об этом минуту, и кажется, что мы на горной охоте в очень сырых условиях. Относительная влажность очень близко до штатных 78%, так что о регулировках там не заморачиваемся.Но температура и атмосферное давление далеко не стандартные.Как они повлияют на снаряженные нами боеприпасы с баллистическим коэффициентом штатного состояния .338?
Очевидный баллистический коэффициент = Поправочный коэффициент температуры x Поправочный коэффициент барометрического давления x Текущий баллистический коэффициент =.942 х 1,406 х 0,338 = 0,448.
С практической точки зрения, более низкая температура сама по себе уменьшит кажущийся баллистический коэффициент, но в сочетании с поправкой на низкое барометрическое давление общим результатом будут более плоские траектории для боеприпасов, принесенных на эту охоту.
Стрелки, которые переходят с малых высот на большие высоты или наоборот, должны взять с собой достаточно боеприпасов для прицеливания своего огнестрельного оружия на новом месте. Плоские траектории, полученные при перезарядке в Форт-Коллинзе, штат Колорадо, могут быть не такими плоскими на охоте в лесах штата Мэн.Стремление выше обычных диапазонов является ответом здесь. И наоборот, при доставке проверенных грузов из Мобила, штат Алабама, в горы Британской Колумбии может потребоваться прицеливание ниже, чем у дома.
Для расстояний до 300 ярдов включительно корректировка баллистических коэффициентов практически не требуется. Стабильность положения для стрельбы и навыки прицеливания стрелка могут объяснить большую разницу между запланированной и фактической траекторией, чем могут потребоваться поправочные коэффициенты.Если реальные условия стрельбы будут резко отличаться от домашних, разумным советом будет взять с собой достаточно патронов, чтобы перезарядить оружие на месте стрельбы.
В сторону энергии
На протяжении многих лет многие авторы уделяли много времени изучению концепции характеристик пули. В матчевых соревнованиях или стрельбе по мишеням стандарты эффективности просты и понятны. Пули для стрельбы по мишеням должны быть высокоэффективными (обтекаемыми, с высоким баллистическим коэффициентом), чтобы стрелять максимально настильно и противостоять ветровому сносу.Однако эффективность не имеет значения, если эти пули также не точны — они сделаны настолько тщательно и точно, что они обычно будут поражать цели с точностью до минуты.
Однако эффективность охотничьих пульпредставляет собой гораздо более сложный вопрос. Некоторые утверждают, что вы должны ожидать найти свою великолепно разросшуюся пулю под шкурой животного напротив входного отверстия. Позор вам, если он не весит б/у 95% от того, что весил новый. Другие говорят, что это нормально, если пуля входит в цель и выходит из нее, пока она наносит смертельный урон на своем пути.Прагматики довольны пулями, которые попадают туда, куда нацелены, и сразу же убивают дичь. Они охотники, утверждают они, а не патологоанатомы.
Производительность зависит только от мнения? Догадок? Такой предмет, как религия и политика, по которому всегда будут разногласия?
Опытный охотник знает, что он никогда не будет получать только идеальные выстрелы в идеальных условиях, когда его снаряжение всегда в превосходной форме, а его винтовка пристреляна на абсолютно правильной дистанции.Вот почему опытный охотник так любит свой спорт. Здесь задействованы его навыки, требуется его рассудительность, всегда требуется его интеллект — и он столкнется с настоящими трудностями в полевых условиях. Ему нужно подготовиться к этим вызовам, как при выборе снаряжения, так и при подготовке к полю. Шансы любого охотника значительно повышаются, когда он выбирает правильное ружье, правильную пулю и правильный заряд для поставленной задачи. Насколько стрелок должен понимать такие переменные, как траектории, эффекты сноса ветром и скорости пули на ожидаемых дистанциях охоты, он также должен думать об энергии, которую пуля будет генерировать при ударе.
Кинетическая энергия пули, измеряемая в футо-фунтах, является показателем того, что обычно называют «останавливающей силой». Предполагалось, что чем выше энергия пули в точке попадания, тем больше ее «останавливающая сила». Здесь есть некоторые предостережения. Пуля полностью высвобождает свою энергию в мишени только в том случае, если она остается в игровом животном. Если у него больше энергии, чем достаточно, он может выполнить свою работу и выйти. Это, конечно, не повод для беспокойства. Если у него недостаточно энергии, чтобы убить, будь то из-за неправильного выбора пули или выстрелов с чрезмерной дальности, это повод для беспокойства.Ответственные охотники должны убедиться, что они могут выполнить работу с помощью выбранных ими инструментов. Стрельба на дистанциях, где пуля не может надежно поразить и убить дичь, является довольно безответственным поведением.
ПулиHornady для варминтинга предназначены для быстрого полета и мгновенного и взрывного высвобождения своей высокой кинетической энергии. Если они будут слишком сильны для конкретного варминта и пройдут дальше, раневой канал и выходное отверстие подтвердят их разрушительную силу.
ПулиHornady для охоты разработаны для надежного и контролируемого расширения во всех конструкциях охотничьих пуль.Ни одна охотничья пуля не может быть максимально эффективной, если она не расширяется до большего диаметра, чем размер ее калибра. Расширение замедляет пулю и позволяет ей терять кинетическую энергию. Все пули Hornady для охоты изготавливаются с элементами InterLock или InterBond, которые соединяют оболочку и сердечник. Это гарантирует, что более тяжелая масса проникнет в игровое животное и распространит внутри него ударные волны. Чем выше конечная скорость пули, тем выше ее конечная энергия. Расширение и проникновение обеспечивают высвобождение энергии, что, в свою очередь, приводит к смертельным результатам — и более верным убийствам.
Это не последнее слово в характеристиках охотничьих пуль. Скорее, мы надеемся стимулировать ваше размышление о предмете и о том, насколько важна конечная энергия пули для производительности. Конечная энергия и превосходная конструкция расширения пули позволяют полностью высвобождать оставшуюся энергию пули внутри охотничьего животного. Hornady Bullets опирается на более чем 60-летний опыт работы в этой области.
Траектория
Будучи снарядом, пуля траектория следует параболической траектории. «Падение пули» это расстояние, на которое траектория проходит ниже осевой линии отверстие. Линия визирования пересекает траекторию в двух расстояния. Расстояния, на которых линия обзора пересекает траектория пули известна как «ноль» оружия. На нуле огнестрельного оружия нет необходимости в вертикальной коррекции. на прицелах огнестрельного оружия.
На рисунке выше при выстреле пуля вылетает из ствола ружья с определенной скоростью, известный как » начальная скорость .«Вертикаль компонента вектора скорости (ось Y) испытывает ускорение под действием силы тяжести в отрицательном направлении оси Y. То вектор скорости испытывает отрицательное ускорение направление из-за сопротивления, когда пуля летит по воздуху. Это сопротивление вызывает повышенное падение пули по отношению к пройденный путь.
Стрельба из Высота
Огнестрельное оружие с горизонтальным нулем ( RH ) будет иметь ноль (RS) , если линия прямой видимости под углом (тета) образуют горизонталь. Правая < RS при 0 < (величина тета) < пи . Таким образом, чтобы поразить цель на расстоянии (RH) , но в направлении (тета) от горизонтали надо целиться ниже. Это не имеет значения при стрельбе по цели на большей высоте соответственно или более низкая высота, в любом случае нужно стремиться ниже.
При съемке под углом (тета) ускорение силы тяжести пули перпендикулярно
к линии сайта, = ( a ) x cos(theta) .Это значение меньше, чем ускорение из-за
гравитация. Перпендикулярно линии сайта, на пуле
при съемке с горизонтальной линии сайта, что = (а) .
Меньшее ускорение означает, что пуля падает с
относительно линии сайта меньше.
Стрельба С движущейся платформы
Стрельба по движущейся мишени требует «вести» себя. цель.Это означает, что необходимо учитывать расстояние до цели, вектор скорости имеет цель, и скорость пули после выстрела.
Стрельба по Движущаяся цель
Стрельба по движущейся цели то же, что и стрельба по движущейся платформе. Единственная разница в том, что
Внешняя баллистика | Military Wiki
Шлирен-изображение пули, летящей в свободном полете, демонстрирующее динамику давления воздуха вокруг пули.
- Внешняя баллистика или Внешняя баллистика — это часть баллистики, изучающая поведение снаряда без двигателя в полете.
Внешняя баллистика часто ассоциируется с огнестрельным оружием и имеет дело с фазой свободного полета пули без двигателя после выхода из ствола и до попадания в цель, поэтому она находится между переходной баллистикой и конечной баллистикой.
Однако внешняя баллистика также связана со свободным полетом ракет и других снарядов, таких как шары, стрелы и т. д.
Силы, действующие на снаряд[]
В полете основными силами, действующими на снаряд, являются гравитация, сопротивление и, если есть, ветер. Гравитация придает снаряду нисходящее ускорение, заставляя его падать с линии прицеливания. Сопротивление или сопротивление воздуха замедляет снаряд с силой, пропорциональной квадрату скорости. Ветер заставляет снаряд отклоняться от траектории. Во время полета гравитация, сопротивление и ветер оказывают большое влияние на траекторию полета снаряда, и их необходимо учитывать при прогнозировании движения снаряда.
Для средних и больших расстояний и продолжительности полета, помимо силы тяжести, сопротивления воздуха и ветра, необходимо учитывать несколько мезопеременных, описанных в параграфе о внешних факторах. Мезо-переменные могут стать важными для пользователей огнестрельного оружия, которым приходится иметь дело со сценариями стрельбы под углом или на больших дистанциях, но редко имеют значение на обычных дистанциях охоты и стрельбы по мишеням.
Для больших и очень больших расстояний и продолжительности полета незначительные эффекты и силы, такие как описанные в параграфе о факторах большой дальности, становятся важными и должны учитываться.Практические эффекты этих переменных, как правило, не имеют значения для большинства пользователей огнестрельного оружия, поскольку нормальный групповой разброс на коротких и средних дистанциях преобладает над влиянием, которое эти эффекты оказывают на траектории снарядов огнестрельного оружия.
На очень больших дистанциях артиллерия должна стрелять снарядами по траекториям, которые даже приблизительно не являются прямыми; они ближе к параболическим, хотя на это влияет сопротивление воздуха.
В случае с баллистическими ракетами существенное влияние оказывают также высоты полета, поскольку часть полета происходит почти в вакууме.
Стабилизация несферических снарядов во время полета[]
Для стабилизации несферических снарядов во время полета можно использовать два метода:
- Снаряды, такие как стрелы или башмаки, такие как M829 Бронебойный, оперенный, отбрасываемый башмак (APFSDS), достигают стабильности, заставляя их центр давления (ЦД) смещаться за их центр тяжести (ЦТ) с хвостовыми поверхностями. ЦТ за условием ЦТ обеспечивает стабильный полет снаряда, то есть снаряд не будет переворачиваться во время полета через атмосферу из-за аэродинамических сил.
- Снаряды, такие как пули стрелкового оружия и артиллерийские снаряды, должны справляться с тем, что их ЦТ находится перед их ЦТ, что дестабилизирует эти снаряды во время полета. Для стабилизации таких снарядов снаряд раскручивается вокруг своей продольной (ведущей к хвостовой) оси. Вращающаяся масса делает ось длины пули устойчивой к дестабилизирующему опрокидывающему моменту ЦД, находящейся перед ЦТ.
Внешняя баллистика стрелкового оружия[]
Падение пули и путь пули[]
Типовой график траектории для карабина M4 и винтовки M16A2 с использованием идентичных патронов M855 с идентичными снарядами.Хотя обе траектории имеют одинаковые 25 м вблизи нуля, разница в начальной скорости снарядов постепенно вызывает значительную разницу траекторий и дальнего нуля. Ось 0 дюймов представляет линию визирования или горизонтальную плоскость визирования.
Влияние гравитации на снаряд в полете часто называют падением пули. Важно понимать влияние силы тяжести при пристрелке прицельных компонентов ружья. Чтобы спланировать падение пули и правильно компенсировать его, необходимо понимать траектории параболической формы.
Падение пули[]
Для того, чтобы снаряд попал в любую удаленную цель, ствол должен быть наклонен на положительный угол возвышения по отношению к цели. Это связано с тем, что снаряд начинает реагировать на действие силы тяжести в тот момент, когда он освобождается от механических ограничений канала ствола. Таким образом, пуля, выпущенная с нулевым углом возвышения, никогда не может попасть в цель выше или на том же возвышении, что и центральная ось канала ствола. Воображаемая линия, идущая вниз от центральной оси канала ствола и уходящая в бесконечность, называется линией вылета и представляет собой линию, по которой пуля покидает ствол.По мере того, как пуля движется вниз по дальности, она огибает дугу ниже линии вылета, поскольку она отклоняется от своего первоначального пути под действием силы тяжести. Падение пули определяется как вертикальное расстояние снаряда ниже линии вылета из канала ствола. Даже когда линия вылета наклонена вверх или вниз, падение пули по-прежнему определяется как расстояние между пулей и линией вылета в любой точке траектории. Таким образом, падение пули не имеет большого практического значения для стрелков, поскольку оно не описывает фактическую траекторию пули и не зависит от направления или расстояния до цели.Его лучше всего описать как промежуточный параметр, наиболее полезный в баллистических расчетах, где он необходим для расчета значений других параметров. Помимо этого, это в основном полезно при проведении прямого сравнения двух разных снарядов по форме их траекторий.
Траектория пули[]
Для поражения удаленной цели требуется соответствующий положительный угол возвышения, который достигается за счет наклона линии прицеливания от глаза стрелка через осевую линию прицельного комплекса вниз к линии стрельбы.Этого можно достичь, просто механически отрегулировав прицел вниз, или закрепив всю прицельную систему на наклонном креплении с известным наклоном вниз, или с помощью комбинации того и другого. Эта процедура приводит к поднятию дульного среза, когда впоследствии необходимо поднять ствол, чтобы совместить прицел с целью. Пуля, вылетающая из дульного среза под заданным углом возвышения, следует по баллистической траектории, характеристики которой зависят от различных факторов, таких как начальная скорость, гравитация и аэродинамическое сопротивление.Эта баллистическая траектория называется траекторией пули.
Траектория пули очень полезна для стрелков, потому что позволяет им составлять баллистические таблицы, которые предсказывают, какая поправка по высоте должна быть применена к линии прицеливания для выстрелов на различных известных дистанциях. Значения пути пули определяются как высотой прицела или расстоянием линии прицеливания над осевой линией канала ствола, так и расстоянием, на котором прицелы обнуляются, что, в свою очередь, определяет угол возвышения.Пуля, летящая по баллистической траектории, совершает как прямое, так и вертикальное движение. Движение вперед замедляется из-за сопротивления воздуха, а при моделировании точечной массы вертикальное движение зависит от комбинации угла места и силы тяжести. Первоначально пуля поднимается относительно линии прицеливания или горизонтальной плоскости прицеливания. В конечном итоге пуля достигает своей вершины (высшей точки параболы траектории), где вертикальная составляющая скорости уменьшается до нуля под действием силы тяжести, а затем начинает опускаться, в конечном итоге ударяясь о землю.Чем дальше расстояние до намеченной цели, тем больше угол места и выше вершина.
Траектория пули дважды пересекает горизонтальную плоскость прицеливания. Ближайшая к оружию точка возникает, когда пуля поднимается по линии прицеливания, и называется ближней нулевой точкой. Вторая точка возникает, когда пуля проходит через линию прицеливания. Он называется дальним нулем и определяет текущий прицел по дальности для пистолета. Траектория пули численно описывается как расстояние выше или ниже горизонтальной плоскости прицеливания в различных точках траектории.Это отличается от падения пули, которое относится к плоскости, содержащей линию вылета, независимо от угла места. Поскольку для каждого из этих двух параметров используются разные исходные данные, может возникнуть значительная путаница, поскольку даже если пуля движется значительно ниже линии вылета, она все равно может набирать реальную и значительную высоту по отношению к линии прицеливания, а также к поверхности. земли в случае горизонтального или почти горизонтального выстрела над ровной местностью.Проще говоря, один параметр (падение пули) сравнивает относительное положение реальной пули с воображаемой пулей, которой не препятствует гравитация, а другой параметр (траектория пули) описывает реальный путь пули через атмосферу Земли с учетом как гравитационные, так и аэродинамические эффекты.
Моделирование и измерение сопротивления лобовому сопротивлению[]
Шлирен-фотография / теневой график оторвавшейся ударной волны или ударной волны вокруг пули в сверхзвуковом полете, опубликованный Эрнстом Махом в 1888 году.
Математические модели для расчета эффектов лобового сопротивления или сопротивления воздуха довольно сложны и часто ненадежны на расстоянии более 500 метров, поэтому наиболее надежным методом определения траекторий по-прежнему остается эмпирическое измерение.
Модели с фиксированной кривой сопротивления, сгенерированные для снарядов стандартной формы[]
Стандартный снаряд формыG1. Все измерения в калибрах/диаметрах.
Использование баллистических таблиц или баллистического программного обеспечения, основанного на модели сопротивления Siacci/Mayevski G1, представленной в 1881 году, является наиболее распространенным методом, используемым для работы с внешней баллистикой.Пули описываются баллистическим коэффициентом, или BC, который сочетает в себе сопротивление воздуха формы пули (коэффициент лобового сопротивления) и плотность ее поперечного сечения (функция массы и диаметра пули).
Замедление из-за сопротивления, которое испытает снаряд массой m , скоростью v и диаметром d , пропорционально 1/BC, 1/ m , v² и d² 9 9 БК дает коэффициент баллистической эффективности по сравнению со стандартным снарядом G1, который имеет вес 1 фунт (454 г), 1 дюйм (25,5 дюйма).Пуля диаметром 4 мм с плоским основанием, длиной 3,28 дюйма (83,3 мм) и радиусом 2 дюйма (50,8 мм) по касательной к острию. Стандартный снаряд G1 происходит от стандартного эталонного снаряда «C», определенного немецким производителем стали, боеприпасов и вооружений Krupp в 1881 году. Стандартный снаряд модели G1 имеет БК 1. [1] Французская комиссия Гавра решила использовать этот снаряд стал их первым эталонным снарядом, получившим название G1. [2] [3]
Спортивные пули, калибром d в диапазоне от 0.От 177 до 0,50 дюймов (от 4,50 до 12,7 мм) коэффициент плавучести G1 находится в диапазоне от 0,12 до чуть более 1,00, при этом 1,00 соответствует наибольшей аэродинамике, а 0,12 — наименьшей. Пули с очень низким лобовым сопротивлением и БК ≥ 1,10 могут быть спроектированы и изготовлены на прецизионных станках с ЧПУ из монометаллических стержней, но ими часто приходится стрелять из изготовленных на заказ полнокалиберных винтовок со специальными стволами. [4]
Плотность сечения является очень важным аспектом пули и представляет собой отношение площади лобовой поверхности (половина квадрата диаметра пули, умноженная на число Пи) к массе пули.Поскольку для данной формы пули лобовая поверхность увеличивается пропорционально квадрату калибра, а масса увеличивается пропорционально кубу диаметра, плотность сечения растет линейно с диаметром канала ствола. Поскольку БК сочетает в себе форму и плотность сечения, модель снаряда G1 в половинном масштабе будет иметь БК 0,5, а модель в четверть масштаба будет иметь БК 0,25.
Поскольку различные формы снарядов по-разному реагируют на изменение скорости (особенно между сверхзвуковой и дозвуковой скоростями), БК, предоставляемый производителем пуль, будет средним БК, представляющим общий диапазон скоростей для этой пули.Для винтовочных пуль это, вероятно, будет сверхзвуковая скорость, для пистолетных пуль, вероятно, будет дозвуковая. Для снарядов, летящих на сверхзвуковых, околозвуковых и дозвуковых режимах полета, BC не может быть хорошо аппроксимирован одной константой, а считается функцией BC(M) числа Маха M; здесь М равно скорости снаряда, деленной на скорость звука. При полете снаряда М будет уменьшаться, а значит (в большинстве случаев) будет уменьшаться и БК.
Большинство баллистических таблиц или программного обеспечения считают само собой разумеющимся, что одна конкретная функция сопротивления правильно описывает сопротивление и, следовательно, летные характеристики пули, связанные с ее баллистическим коэффициентом. Эти модели не делают различий между типами или формами пули с пыжом, плоским основанием, спитцером, хвостовой частью, очень низким лобовым сопротивлением и т. д. Они предполагают одну неизменную функцию сопротивления, как указано в опубликованном BC.
Однако доступны несколько моделей кривых сопротивления, оптимизированных для нескольких стандартных форм снарядов.Полученные в результате модели с фиксированной кривой сопротивления для нескольких стандартных форм или типов снарядов называются:
Стандартный снаряд формы G7. Все измерения в калибрах/диаметрах.
- G1 или Ingalls (плоское основание с 2-х калибровым (тупым) носовым оживом — безусловно, самое популярное)
- G2 (снаряд Aberdeen J)
- G5 (короткая лодочка 7,5°, длинная касательная оживальная часть 6,19 калибра)
- G6 (плоское основание, длинный секущий оживальный элемент 6 калибров)
- G7 (длинный 7.5° лодочка, тангенциальный ожив 10 калибров, предпочтительный для некоторых производителей пуль с очень низким лобовым сопротивлением [5] )
- G8 (плоская база, 10 калибров, длинная секущая оживальная часть)
- GL (тупой свинцовый наконечник)
Как различные режимы скорости влияют на винтовочные пули калибра .338, можно увидеть в брошюре о продукте .338 Lapua Magnum, в которой говорится, что доплеровский радар установил данные BC G1. [6] [7] Причина публикации данных, как в этой брошюре, заключается в том, что модель Сиаччи/Маевского G1 не может быть настроена на поведение сопротивления конкретного снаряда, форма которого значительно отличается от формы используемого эталонного снаряда.Некоторые разработчики баллистического программного обеспечения, которые основывали свои программы на модели Сиаччи/Маевского G1, дают пользователю возможность вводить несколько различных констант БК G1 для различных режимов скорости, чтобы рассчитать баллистические прогнозы, которые более точно соответствуют поведению пули при полете на больших расстояниях по сравнению с расчетами. которые используют только одну константу BC.
Приведенный выше пример иллюстрирует основную проблему моделей с фиксированной кривой сопротивления. Эти модели будут давать удовлетворительные точные прогнозы только в том случае, если интересующий снаряд имеет ту же форму, что и эталонный снаряд, или форму, очень похожую на эталонный снаряд.Любое отклонение от эталонной формы снаряда приведет к менее точным прогнозам. [8] Степень отклонения снаряда от применяемого эталонного снаряда математически выражается форм-фактором ( i ). [9] Форм-фактор можно использовать для сравнения сопротивления интересующего снаряда с сопротивлением используемого эталонного снаряда при заданной скорости (дальности). Проблема, заключающаяся в том, что фактическая кривая сопротивления снаряда может значительно отклоняться от фиксированной кривой сопротивления любого используемого эталонного снаряда, систематически ограничивает традиционный подход к моделированию сопротивления сопротивлению.Относительная простота, однако, позволяет объяснить и понять его широкой публике, занимающейся стрельбой, и, следовательно, он также популярен среди разработчиков баллистического программного обеспечения для прогнозирования и производителей пуль, которые хотят продавать свою продукцию.
Более продвинутые модели для перетаскивания[]
Модель Пейса[]
Помимо традиционных моделей кривой сопротивления для нескольких стандартных форм или типов снарядов существуют и другие, более совершенные модели сопротивления. Наиболее известной альтернативной баллистической моделью, вероятно, является модель, представленная в 1980 г.Артур Дж. Пейса. Г-н Пейса утверждает на своем веб-сайте, что его метод неизменно позволял прогнозировать (сверхзвуковые) траектории винтовочных пуль в пределах 2,5 мм (0,1 дюйма) и скорости пуль в пределах 0,3 м/с (1 фут/с) на расстоянии до 914 м (1000 ярдов). по сравнению с десятками реальных измерений. [10] Модель Пейса представляет собой решение закрытой формы, для которого не требуется использование каких-либо таблиц или фиксированных кривых сопротивления, созданных для снарядов стандартной формы.
Самая сильная сторона модели Пейсы заключается в том, что любой снаряд в заданном режиме полета (например, в режиме сверхзвукового полета) может быть математически хорошо смоделирован только с двумя измерениями скорости, расстоянием между указанными измерениями скорости и постоянным коэффициентом наклона или замедления. [11] Модель позволяет кривой сопротивления изменять наклон или кривизну в трех разных точках. [12] Данные измерения скорости на дальнем расстоянии могут быть предоставлены вокруг ключевых точек перегиба, что позволяет более точно рассчитать скорость замедления снаряда. Модель Пейсы позволяет настраивать коэффициент наклона для учета тонких различий в скорости замедления пуль разных форм и размеров. Он колеблется от 0,1 (плосконосые пули) до 0,9 (пули с очень низким лобовым сопротивлением).Если этот коэффициент наклона или константы замедления неизвестен, значение по умолчанию, равное 0,5, будет достаточно хорошо предсказывать поведение большинства современных винтовочных пуль типа «спитцер». С помощью тестовых стрельб можно определить постоянную наклона для конкретной комбинации пуля/винтовка/стрелок. Эти испытательные стрельбы желательно проводить на 60%, а для прогнозирования экстремально дальней баллистики также на 80-90% сверхзвуковой дальности интересующих снарядов, избегая неустойчивых околозвуковых эффектов.Благодаря этому модель Пейсы можно легко настроить для конкретного поведения сопротивления конкретного снаряда, что делает возможными значительно лучшие (сверхзвуковые) баллистические прогнозы для дальностей более 500 м (547 ярдов). Практическим недостатком модели Пейсы является то, что подавляющее большинство любителей стрельбы не может легко выполнить точные измерения скорости снаряда на дальнем расстоянии, чтобы обеспечить эти более точные прогнозы.
Средний коэффициент замедления может быть рассчитан для любого заданного постоянного коэффициента уклона, если известны точки данных скорости и известно расстояние между указанными измерениями скорости.Очевидно, это справедливо только в пределах одного и того же режима полета. Под скоростью понимается фактическая скорость, так как скорость есть векторная величина, а скорость есть величина вектора скорости. Поскольку степенная функция не имеет постоянной кривизны, нельзя использовать простое хордовое среднее. В модели Pejsa используется средневзвешенный коэффициент замедления, взвешенный по дальности 0,25. Более близкая скорость имеет больший вес. Коэффициент замедления измеряется в футах, тогда как дальность измеряется в ярдах, следовательно, 0.25 * 3,0 = 0,75, местами используется 0,8, а не 0,75. 0,8 получается из-за округления, чтобы упростить ввод в ручных калькуляторах. Поскольку в модели Пейсы не используется простое взвешенное среднее по хорде, два измерения скорости используются для нахождения среднего коэффициента хордового замедления на среднем расстоянии между двумя точками измерения скорости. Чтобы найти начальный коэффициент замедления, доктор Пейса приводит два отдельных уравнения в своих двух книгах. Первая связана с функцией мощности. [13] Второе уравнение идентично тому, которое использовалось для нахождения средневзвешенного значения при R/4; добавьте N * (R/2), где R — расстояние в футах, к среднему коэффициенту замедления по хорде на средней дистанции, а N — постоянный коэффициент уклона. [14] После определения стартового коэффициента замедления используется обратная процедура для нахождения средневзвешенного значения при R / 4; начальный коэффициент замедления минус N * (R/4). Другими словами, N используется как наклон хорды.Доктор Пейса утверждает, что он расширил свою формулу падения в степенной ряд, чтобы доказать, что средневзвешенный коэффициент замедления при R/4 является хорошим приближением. Для этого доктор Пейса сравнил разложение по степеням своей формулы капель с разложением мощности какой-то другой неназванной формулы капель, чтобы прийти к своим выводам. Четвертый член в обоих степенных рядах совпадал, когда коэффициент замедления в диапазоне 0,25 использовался в формуле падения Пейсы. Четвертый термин был также первым термином, в котором использовалась Н.Более высокие члены, включающие N, были незначительными и исчезали при N = 0,36, что, по словам доктора Пейсы, было удачным совпадением, обеспечивающим чрезвычайно точную линейную аппроксимацию, особенно для N около 0,36. Если используется функция коэффициента запаздывания, можно получить точные средние значения для любого N, потому что с помощью исчисления легко найти среднее значение любой интегрируемой функции. [15] Д-р Пейса утверждает, что коэффициент замедления может быть смоделирован как C * V N , где C — подгоночный коэффициент, который исчезает при выводе формулы падения, а N — постоянный коэффициент наклона. [16] Коэффициент замедления равен квадрату скорости, деленному на коэффициент замедления A. Использование среднего коэффициента замедления позволяет модели Пейсы быть выражением в замкнутой форме в рамках заданного режима полета.
Чтобы можно было использовать баллистический коэффициент G1, а не данные о скорости, доктор Пейса предоставил две эталонные кривые сопротивления. Первая эталонная кривая сопротивления основана исключительно на функции коэффициента замедления Сиаччи/Маевского. Вторая эталонная кривая сопротивления скорректирована, чтобы соответствовать функции коэффициента замедления Сиаччи/Маевского при скорости снаряда 2600 футов в секунду (792.5 м/с) с использованием патрона .30-06 Springfield, шарика, калибра .30 M2 152 гран (9,8 г) винтовочной спитцерной пули с постоянным коэффициентом наклона или замедления 0,5 в сверхзвуковом режиме полета. В других режимах полета вторая модель эталонной кривой лобового сопротивления Пейсы использует постоянные коэффициенты наклона 0,0 или -4,0. Эти постоянные коэффициенты замедления можно проверить, изменив формулы Пейсы (участки кривой сопротивления соответствуют форме V (2 — N) / C, а участки кривой коэффициента замедления соответствуют форме V 2 / (V (2 — N) / C) = C * V N , где C — коэффициент подгонки).Данные эмпирических испытаний, которые Пейса использовал для определения точной формы выбранной им эталонной кривой сопротивления, и предварительно определенная математическая функция, которая возвращает коэффициент замедления при заданном числе Маха, были предоставлены военными США для пули Cartridge, Ball, Caliber .30 M2. . Расчет функции коэффициента замедления также включает плотность воздуха, о которой Пейса не упомянул явно. Модель Siacci/Mayevski G1 использует следующую параметризацию замедления (60 °F, 30 дюймов ртутного столба и влажность 67 %, плотность воздуха ρ = 1.2254 кг/м 3 ). [17] Доктор Пейса предлагает использовать вторую кривую аэродинамического сопротивления, поскольку кривая аэродинамического сопротивления Siacci/Mayevski G1 не подходит для современных спитцеровских пуль. [18] Чтобы получить соответствующие коэффициенты замедления для оптимального моделирования дальнего действия, д-р Пейса предложил использовать точные данные измерения скорости на дальнем расстоянии для конкретного снаряда для эмпирического расчета среднего коэффициента замедления, а не использовать средний коэффициент замедления, полученный по эталонной кривой сопротивления. .Кроме того, он предложил использовать боеприпасы с уменьшенной пороховой нагрузкой для эмпирической проверки фактического поведения снаряда при полете на более низких скоростях. При работе с уменьшенными пороховыми зарядами необходимо соблюдать крайнюю осторожность, чтобы избежать опасных или катастрофических условий (детонации), которые могут возникнуть при стрельбе экспериментальными зарядами из огнестрельного оружия. [12]
Некоторые разработчики программного обеспечения предлагают коммерческое программное обеспечение, основанное на модели сопротивления Пейса, дополненной и улучшенной с учетом обычно незначительных эффектов (Кориолис, гироскопический дрейф и т. д.).), которые вступают в игру на дальних дистанциях. Разработчики этих программ, основанных на модели Пейсы, усовершенствовали исходные алгоритмы Пейсы, используя итерационные или рекурсивные математические подходы для каждого сегмента кривой коэффициента замедления с другим коэффициентом наклона N, для более достоверных баллистических прогнозов за пределами 1000 м (1094 ярда), где мощные винтовочные пули с очень низким лобовым сопротивлением имеют тенденцию становиться околозвуковыми и, в конечном итоге, дозвуковыми. [19] [20] Эти программы, основанные на модели Пейса, могут также позволять использовать средний коэффициент замедления, полученный из данных о скорости, поскольку Dr.Оригинальное баллистическое программное обеспечение Пейсы сделало это. Кроме того, эти другие разработчики баллистического программного обеспечения, основанные на модели Пейсы, могут произвольно выбрать другие эталонные переменные снаряда, скорости и / или плотности воздуха, чем доктор Пейса использовал для изменения математической функции сопротивления или сделать свое программное обеспечение подходящим для использования баллистического коэффициента, отличного от G1. .
Модель Manges[]
Хотя она и не так известна, как модель Пейса, дополнительная альтернативная баллистическая модель была представлена в 1989 году полковником Даффом Мангесом (армия США в отставке) на 11-м Международном баллистическом симпозиуме по подготовке американской обороны (ADPA), проходившем в Брюссельском конгресс-центре, Брюссель, Бельгия, 9–11 мая 1989 г.Статья под названием «Решения по траектории закрытой формы для систем оружия прямой наводки» появляется в материалах, Том 1, Динамика движения, Динамика запуска, Динамика полета, страницы 665-674. Первоначально задуманная для моделирования сопротивления снаряда для 120-мм танковых боеприпасов, новая формула коэффициента сопротивления была впоследствии применена к баллистическим траекториям винтовочных боеприпасов центрального воспламенения с результатами, сравнимыми с результатами, заявленными для модели Pejsa.
Модель Manges использует теоретический подход первых принципов, который избегает кривых «G» и «баллистических коэффициентов», основанных на стандартной G1 и других кривых подобия.Теоретическое описание состоит из трех основных частей. Во-первых, разработать и решить формулировку двумерных дифференциальных уравнений движения, определяющих плоские траектории снарядов с точечной массой, путем математического определения набора квадратур, которые допускают решения в замкнутой форме для траекторных дифференциальных уравнений движения. Генерируется последовательность функций коэффициента сопротивления последовательного приближения, которые быстро сходятся к фактически наблюдаемым данным сопротивления. Вакуумная траектория, упрощенная аэродинамика, модели закона сопротивления Д’Антонио и Эйлера являются частными случаями.Таким образом, закон сопротивления Манжа обеспечивает объединяющее влияние по отношению к более ранним моделям, которые использовались для получения двумерных решений в замкнутой форме для уравнений движения точечной массы. Третья цель этой статьи состоит в том, чтобы описать процедуру подгонки по методу наименьших квадратов для получения новых функций сопротивления из наблюдаемых экспериментальных данных. Автор утверждает, что результаты показывают отличное совпадение с численными расчетами с шестью степенями свободы для современных танковых боеприпасов и доступными опубликованными таблицами стрельбы для винтовочных боеприпасов центрального воспламенения, имеющих самые разные формы и размеры.
Было разработано приложение Microsoft Excel, в котором используются аппроксимации методом наименьших квадратов полученных в аэродинамической трубе табличных коэффициентов сопротивления. В качестве альтернативы производитель может предоставить баллистические данные о траектории или данные о скорости, полученные в доплеровском режиме, для калибровки модели. Затем приложение Excel использует пользовательские макрокоманды для расчета интересующих переменных траектории. Используется модифицированный алгоритм интегрирования Рунге-Кутты 4-го порядка. Как и Пейса, полковник Манжес заявляет о точности винтовки центрального воспламенения с точностью до одной десятой дюйма для положения пули и с точностью до фута в секунду для скорости снаряда.
С материалами 11-го Международного баллистического симпозиума можно ознакомиться через Национальную оборонную промышленную ассоциацию (NDIA) на веб-сайте http://www.ndia.org/Resources/Pages/Publication_Catalog.aspx.
Модель с 6 степенями свободы (6 степеней свободы)[]
Также доступны профессиональные баллистические модели, такие как PRODAS. Они основаны на расчетах 6 степеней свободы (6 DoF). 6 Моделирование степени свободы требует таких сложных входных данных, знания используемых снарядов и длительного времени расчета на компьютерах, что нецелесообразно для непрофессиональных баллистиков и использования в полевых условиях, когда расчеты, как правило, должны выполняться на лету на мобильных вычислительных устройствах, таких как (защищенные) КПК. или смартфоны с относительно скромной вычислительной мощностью.6 DoF обычно используется военными организациями, изучающими баллистическое поведение ограниченного числа (предназначенных) военных снарядов. Рассчитанные тренды 6 степеней свободы могут быть включены в виде поправочных таблиц в более традиционные баллистические программные приложения.
Доплеровские радиолокационные измерения[]
Для точного определения эффектов аэродинамического сопротивления или аэродинамического сопротивления снарядов требуются доплеровские радиолокационные измерения. Доплеровские радары Weibel 1000e используются правительствами, профессиональными баллистами, силами обороны и некоторыми производителями боеприпасов для получения реальных данных о поведении интересующих их снарядов в полете.Правильно установленные современные доплеровские радиолокационные измерения могут определять поведение снарядов размером с пневматическую пушку в трехмерном пространстве с точностью до нескольких миллиметров. Собранные данные о замедлении снаряда могут быть получены и выражены несколькими способами, такими как баллистические коэффициенты (BC) или коэффициенты лобового сопротивления (C d ).
Результаты измерений с помощью доплеровского радара для монолитной цельной пули калибра .50 BMG с очень низким лобовым сопротивлением, обработанной на токарном станке (Lost River J40 .510-773 гран монолитная сплошная пуля / скорость кручения 1:15 дюйма) выглядит следующим образом:
| Диапазон (м) | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | 1200 | 1300 | 1400 | 1500 | 1600 | 1700 | 1800 | 1900 | 2000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Баллистический коэффициент | 1.040 | 1,051 | 1,057 | 1,063 | 1,064 | 1,067 | 1,068 | 1,068 | 1,068 | 1,066 | 1,064 | 1,060 | 1,056 | 1,050 | 1,042 | 1,032 |
Начальное увеличение значения БК связано с постоянно присутствующим рысканием и прецессией снаряда из канала ствола. Результаты испытаний были получены из многих выстрелов, а не только из одного выстрела.Производитель пули Lost River Ballistic Technologies присвоил пуле номер 1,062 по номеру БК.
Результаты измерения доплеровским радаром для пули Lapua GB528 Scenar 19,44 г (300 г) калибра 8,59 мм (0,338 дюйма) с очень низким лобовым сопротивлением выглядят следующим образом:
| Число Маха | 0,000 | 0,400 | 0,500 | 0,600 | 0,700 | 0,800 | 0,825 | 0,850 | 0,875 | 0.900 | 0,925 | 0,950 | 0,975 | 1.000 | 1,025 | 1,050 | 1,075 | 1.100 | 1,150 | 1.200 | 1.300 | 1.400 | 1.500 | 1.600 | 1.800 | 2.000 | 2.200 | 2.400 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Коэффициент аэродинамического сопротивления | 0,230 | 0,229 | 0,200 | 0.171 | 0,164 | 0,144 | 0,141 | 0,137 | 0,137 | 0,142 | 0,154 | 0,177 | 0,236 | 0,306 | 0,334 | 0,341 | 0,345 | 0,347 | 0,348 | 0,348 | 0,343 | 0,336 | 0,328 | 0,321 | 0,304 | 0,292 | 0,282 | 0.270 |
Максимальный коэффициент аэродинамического сопротивления испытанной пули достигается при выходе на околозвуковой режим полета на скорости около 1200 Маха.
Общие тенденции аэродинамического сопротивления или баллистического коэффициента[]
Как правило, остроконечная пуля будет иметь лучший коэффициент лобового сопротивления (C d ) или баллистический коэффициент (BC), чем пуля с круглым носом, а пуля с круглым носом будет иметь лучший C d или BC, чем пуля с плоским наконечником. пуля. Кривые большого радиуса, приводящие к меньшему углу при вершине, будут создавать меньшее сопротивление, особенно на сверхзвуковых скоростях.Пули с полым наконечником ведут себя так же, как плоские наконечники того же диаметра. Пули, предназначенные для сверхзвукового использования, часто имеют слегка суженное основание сзади, называемое лодочкой , что снижает сопротивление воздуха в полете. [21] Каннелюры , представляющие собой утопленные кольца вокруг пули, используемые для надежного обжатия пули в гильзе, вызывают увеличение сопротивления.
Трансзвуковая задача[]
Когда скорость винтовочной пули, выпущенной со сверхзвуковой дульной скоростью, приближается к скорости звука, она входит в трансзвуковую область (около 1 Маха.2–0,8). В околозвуковой области центр давления (ЦД) большинства пуль смещается вперед по мере замедления пули. Это смещение CP влияет на (динамическую) стабильность пули. Если пуля плохо стабилизирована, она не может оставаться направленной вперед в околозвуковой области (пули начинают демонстрировать нежелательную прецессию или конусообразное движение, которое, если его не демпфировать, может в конечном итоге закончиться неконтролируемым кувырком вдоль оси длины). Однако, даже если пуля имеет достаточную стабильность (статическую и динамическую), чтобы иметь возможность пролететь околозвуковую область и оставаться направленной вперед, это все равно влияет на нее.Неустойчивый и внезапный сдвиг ЦД и (временное) снижение динамической стабильности могут вызвать значительное рассеивание (и, следовательно, значительное снижение точности), даже если полет пули снова становится нормальным, когда она входит в дозвуковую область. Это очень затрудняет точное предсказание баллистического поведения пуль в околозвуковой области. Кроме того, плотность окружающего воздуха оказывает значительное влияние на динамическую устойчивость во время околозвукового перехода. Хотя плотность окружающего воздуха является переменным фактором окружающей среды, неблагоприятные эффекты околозвукового перехода могут быть лучше нейтрализованы при движении пуль через менее плотный воздух, чем при движении через более плотный воздух.Из-за этого стрелки обычно ограничиваются поражением целей в пределах сверхзвукового диапазона используемой пули. [примечание 1]
Исследование управляемых снарядов[]
Чтобы обойти околозвуковые проблемы, с которыми сталкиваются снаряды со стабилизированным вращением, снаряды стрелкового оружия теоретически могут управляться во время полета. Национальная лаборатория Sandia объявила в январе 2012 года, что она исследовала и провела испытания прототипа самонаводящихся пуль длиной 4 дюйма (102 мм) для мелкокалиберного гладкоствольного огнестрельного оружия, которые могут поражать цели, обозначенные лазером, на расстоянии более более мили (около 2000 метров).Эти снаряды не стабилизированы вращением, и траектория полета может корректироваться с помощью электромагнитного привода 30 раз в секунду. Исследователи также заявляют, что у них есть видео, на котором пуля резко качается при выходе из ствола и меньше качается по мере того, как летит по дальности — спорное явление, известное экспертам по огнестрельному оружию дальнего действия как «засыпание». По словам исследователя из Sandia Рэда Джонса, поскольку движение пули стабилизируется, чем дольше она находится в полете, точность повышается на больших дистанциях. «Никто никогда этого не видел, но у нас есть высокоскоростная видеосъемка, которая показывает, что это правда», — сказал он. [22] Поскольку Sandia ищет партнера из частной компании для завершения испытаний прототипа и вывода управляемой пули на рынок, будущее этой технологии остается неопределенным.
Тестирование прогностических качеств программного обеспечения[]
Из-за практической невозможности узнать заранее и компенсировать все переменные полета, никакое программное моделирование, каким бы совершенным оно ни было, не даст прогнозов, которые всегда будут точно соответствовать траекториям реального мира. Однако можно получить прогнозы, очень близкие к фактическому поведению в полете.
Эмпирический метод измерения[]
Компьютерные программы баллистического прогнозирования, предназначенные для (чрезвычайно) больших расстояний, могут быть оценены путем проведения полевых испытаний на переходном диапазоне от сверхзвукового к дозвуковому (последние 10–20% сверхзвукового диапазона комбинации винтовка/патрон/пуля). Например, для типичной винтовки Lapua Magnum калибра .338, стреляющей стандартными пулями Lapua Scenar GB488 массой 16,2 г (250 г) с начальной скоростью 905 м/с (2969 фут/с), полевые испытания программного обеспечения следует проводить при ≈ 1200–1300 метров (1312 — 1422 ярда) в соответствии с международными стандартами атмосферы на уровне моря (плотность воздуха ρ = 1.225 кг/м³). Чтобы проверить, насколько хорошо программное обеспечение предсказывает траекторию на малой и средней дальности, необходимо провести полевые испытания на 20, 40 и 60% сверхзвуковой дальности. На этих коротких и средних дистанциях околозвуковые проблемы и, следовательно, беспорядочный полет пули не должны возникать, а БК с меньшей вероятностью будет неустойчивым. Тестирование прогностических качеств программного обеспечения на (чрезвычайно) дальних дистанциях стоит дорого, потому что оно требует боеприпасов; фактическая начальная скорость всех выстрелов должна быть измерена, чтобы иметь возможность делать статистически достоверные выводы.Выборочные группы из менее чем 24 выстрелов не дают статистически достоверных данных.
Метод измерения доплеровского радара[]
Правительства, профессиональные баллисты, силы обороны и некоторые производители боеприпасов могут использовать доплеровские радары для получения точных реальных данных о поведении конкретных снарядов, представляющих их интерес, и затем сравнивать собранные реальные данные с прогнозами, рассчитанными баллистическими компьютерными программами. . Однако обычный энтузиаст стрельбы или аэродинамики не имеет доступа к таким дорогим профессиональным измерительным приборам.Власти и производители снарядов, как правило, неохотно делятся с широкой общественностью результатами испытаний доплеровского радара и полученными в ходе испытаний коэффициентами лобового сопротивления (C d ) снарядов.
В январе 2009 года финский производитель боеприпасов Lapua опубликовал данные о коэффициенте лобового сопротивления, полученные в результате испытаний доплеровского радара, для большинства своих винтовочных снарядов. [23] [24] С помощью этого C d специалисты по обработке данных могут создавать алгоритмы, которые используют как известные математические баллистические модели, так и тестовые табличные данные одновременно.При использовании программного обеспечения для прогнозирования, такого как QuickTARGET Unlimited, Lapua Edition [25] или Lapua Ballistics [26] , данные коэффициента сопротивления, полученные в результате испытаний доплеровского радара, могут использоваться для более точных внешних баллистических прогнозов.
Некоторые данные коэффициента лобового сопротивления, предоставленные Lapua, показывают резкое увеличение измеренного лобового сопротивления вокруг или ниже области скорости полета 1 Маха. Такое поведение наблюдалось для большинства измеренных пуль малого калибра и в меньшей степени для пуль большего калибра.Это означает, что некоторые винтовочные пули (в основном меньшего калибра) демонстрировали конусность и/или кувыркание в трансзвуковом/дозвуковом режиме скорости полета. Важна информация о неблагоприятном трансзвуковом/дозвуковом поведении некоторых испытанных снарядов. Это ограничивающий фактор для стрельбы на дальние дистанции, потому что последствия конусообразования и акробатики трудно предсказуемы и потенциально катастрофичны для лучших моделей баллистического прогнозирования и программного обеспечения.
Представленные данные C d не могут быть просто использованы для каждой комбинации пушка-боеприпас, поскольку они были измерены для стволов, скорости вращения (вращения) и партии боеприпасов, которые испытатели Lapua использовали во время своих испытательных стрельб.Такие переменные, как различия в нарезах (количество канавок, глубина, ширина и другие размерные характеристики), скорость закручивания и / или начальная скорость пули, придают снарядам разные скорости вращения (вращения) и следы нарезов. Изменения в таких переменных и вариациях партий выпускаемых снарядов могут привести к различному взаимодействию нижнего диапазона с воздухом, через который проходит снаряд, что может привести к (незначительным) изменениям в поведении полета. Эта конкретная область внешней баллистики в настоящее время (2009 г.) недостаточно изучена и недостаточно изучена. [27]
Прогнозы нескольких методов моделирования и измерения сопротивления лобовому сопротивлению[]
Метод, используемый для моделирования и прогнозирования внешнего баллистического поведения, может давать разные результаты при увеличении дальности и времени полета. Чтобы проиллюстрировать это, несколько методов прогнозирования внешнего баллистического поведения для винтовочной пули Lapua Scenar GB528 весом 19,44 г (300 г) калибра 8,59 мм (0,338 дюйма) с очень низким лобовым сопротивлением и заявленным производителем баллистическим коэффициентом G1 (BC) 0,785 при выстреле на 830 м. Начальная скорость пули в секунду (2723 фута/с) в условиях уровня моря в соответствии с Международными стандартами атмосферы (плотность воздуха ρ = 1,225 кг/м³), 1 Маха = 340,3 м/с), предсказал это для скорости снаряда и времени полета от 0 до 3000 м (от 0 до 3281 ярда): [примечание 2]
| Диапазон (м) | 0 | 300 | 600 | 900 | 1 200 | 1 500 | 1800 | 2 100 | 2400 | 2700 | 3000 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Коэффициенты аэродинамического сопротивления, полученные методом V (м/с) | 830 | 711 | 604 | 507 | 422 | 349 | 311 | 288 | 267 | 247 | 227 |
| Время полета (с) | 0.0000 | 0,3918 | 0,8507 | 1,3937 | 2,0435 | 2,8276 | 3,7480 | 4,7522 | 5,8354 | 7.0095 | 8.2909 |
| Общий перепад (м) | 0,000 | 0,715 | 3.203 | 8.146 | 16.571 | 30.035 | 50.715 | 80.529 | 121.023 | 173,998 | 241.735 |
| Метод сопротивления модели G1 V (м/с) | 830 | 718 | 615 | 522 | 440 | 374 | 328 | 299 | 278 | 261 | 248 |
| Время полета (с) | 0,0000 | 0,3897 | 0,8423 | 1,3732 | 2,0009 | 2,7427 | 3,6029 | 4,5642 | 5.6086 | 6,7276 | 7,9183 |
| Общий перепад (м) | 0,000 | 0,710 | 3,157 | 7,971 | 16.073 | 28.779 | 47.810 | 75.205 | 112,136 | 160.739 | 222 430 |
| Метод сопротивления модели Пейса V (м/с) | 830 | 712 | 603 | 504 | 413 | 339 | 297 | 270 | 247 | 227 | 208 |
| Время полета (с) | 0.0000 | 0,3902 | 0,8479 | 1,3921 | 2.0501 | 2,8556 | 3,8057 | 4,8682 | 6.0294 | 7,2958 | 8,6769 |
| Общий перепад (м) | 0,000 | 0,719 | 3,198 | 8.129 | 16.580 | 30.271 | 51.582 | 82.873 | 126.870 | 185,318 | 260.968 |
| Метод сопротивления модели G7 V (м/с) | 830 | 713 | 606 | 508 | 418 | 339 | 303 | 283 | 265 | 249 | 235 |
| Время полета (с) | 0,0000 | 0,3912 | 0,8487 | 1.3901 | 2.0415 | 2.8404 | 3,7850 | 4.8110 | 5.9099 | 7,0838 | 8.3369 |
| Общий перепад (м) | 0,000 | 0,714 | 3.191 | 8.109 | 16.503 | 30.039 | 51.165 | 81.863 | 123 639 | 178.082 | 246,968 |
Таблица показывает, что традиционный метод прогнозирования модели кривой сопротивления Сиаччи/Маевского G1 обычно дает более оптимистичные результаты по сравнению с современным методом прогнозирования коэффициентов сопротивления (C d ), полученных в ходе доплеровского радиолокационного исследования. [примечание 3] На дальности 300 м (328 ярдов) различия будут малозаметны, но на дальности 600 м (656 ярдов) и выше различия возрастают при скорости снаряда более 10 м/с (32,8 фут/с) и постепенно становятся значительный. На дальности 1500 м (1640 ярдов) прогнозы скорости снаряда отклоняются на 25 м/с (82,0 фута/с), что соответствует прогнозируемой разнице общего падения в 125,6 см (49,4 дюйма) или 0,83 мрад (2,87 МОА) на 50° широты. .
Метод прогнозирования решения в закрытой форме модели сопротивления Пейса без точной настройки коэффициента постоянного наклона дает очень похожие результаты в режиме сверхзвукового полета по сравнению с методом прогнозирования коэффициентов сопротивления, полученных в результате испытания доплеровского радара (C d ).На дальности 1500 м (1640 ярдов) прогнозы скорости снаряда отклоняются на 10 м/с (32,8 фута/с), что соответствует прогнозируемой разнице общего падения в 23,6 см (9,3 дюйма) или 0,16 мрад (0,54 МОА) на 50° широты. .
Метод прогнозирования модели кривой лобового сопротивления G7 (рекомендуемый некоторыми производителями для винтовочных пуль с очень низким лобовым сопротивлением) при использовании баллистического коэффициента (BC) G7, равного 0,377, дает очень похожие результаты в сверхзвуковом режиме полета по сравнению с испытанием доплеровского радара. метод прогнозирования производных коэффициентов лобового сопротивления (C d ).На дальности 1500 м (1640 ярдов) прогнозы скорости снаряда имеют максимальное отклонение 10 м/с (32,8 фута/с). Прогнозируемая общая разница падения на высоте 1500 м (1640 ярдов) составляет 0,4 см (0,16 дюйма) на широте 50 °. Прогнозируемая общая разница падения на высоте 1800 м (1969 ярдов) составляет 45,0 см (17,7 дюйма), что соответствует 0,25 мрад (0,86 МОА).
Внешние факторы[]
Ветер[]
Ветер имеет ряд эффектов, первый из которых заставляет пулю отклоняться в сторону. С научной точки зрения, «ветер, толкающий пулю сбоку», не является причиной сноса пули ветром.Причиной сноса ветром является сопротивление. Сопротивление заставляет пулю разворачиваться против ветра, удерживая центр давления воздуха на носу. Это приводит к тому, что нос поворачивается (с вашей точки зрения) против ветра, а основание взводится (с вашей точки зрения) «по ветру». Итак, (опять же с вашей точки зрения) сопротивление толкает пулю по ветру, заставляя пули следовать за ветром.
Несколько менее очевидный эффект вызывается встречным или попутным ветром. Встречный ветер немного увеличивает относительную скорость снаряда, увеличивает сопротивление и соответствующее падение.Попутный ветер уменьшит лобовое сопротивление и падение пули. В реальном мире чистый встречный или попутный ветер встречается редко, поскольку ветер редко бывает постоянным по силе и направлению и обычно взаимодействует с местностью, над которой дует. Это часто затрудняет стрельбу на сверхдальние дистанции при встречном или попутном ветре.
Вертикальные уголки[]
Вертикальный угол (или возвышение) выстрела также влияет на траекторию выстрела. Баллистические таблицы для снарядов малого калибра (выстреливаемых из пистолетов или винтовок) предполагают, что гравитация действует почти перпендикулярно траектории пули.Если угол направлен вверх или вниз, то перпендикулярное ускорение фактически будет меньше. Влияние компонента траекторного ускорения будет незначительным, поэтому стрельба вверх или вниз по склону приведет к одинаковому уменьшению падения пули.
Часто модели математического баллистического прогнозирования ограничиваются сценариями «плоского огня», основанными на правиле стрелка, что означает, что они не могут давать достаточно точные прогнозы в сочетании с крутыми углами возвышения от -15 до 15 градусов и более длинными дальностями.Однако существует несколько доступных моделей математического прогнозирования для сценариев наклонного пожара, которые дают довольно разные уровни ожидаемой точности. [28]
Плотность окружающего воздуха[]
Колебания давления, температуры и влажности воздуха составляют плотность окружающего воздуха. Влажность оказывает контринтуитивное воздействие. Поскольку плотность водяного пара составляет 0,8 грамма на литр, а плотность сухого воздуха в среднем составляет около 1,225 грамма на литр, более высокая влажность фактически снижает плотность воздуха и, следовательно, уменьшает сопротивление.
Коэффициенты дальнего действия[]
Гироскопический дрейф (Спиновый дрейф)[]
Гироскопический снос — это взаимодействие массы и аэродинамики пули с атмосферой, в которой она летит. Даже в совершенно спокойном воздухе, при полном отсутствии бокового движения воздуха, снаряд со стабилизированным вращением будет испытывать боковую составляющую, вызванную вращением. Для правостороннего (по часовой стрелке) направления вращения этот компонент всегда будет справа. Для левого (против часовой стрелки) направления вращения этот компонент всегда будет слева.Это связано с тем, что продольная ось снаряда (его ось вращения) и направление вектора скорости центра тяжести (ЦТ) отклоняются на небольшой угол, который называется равновесным рысканием или рысканием покоя. Величина угла рыскания и естественного откоса обычно составляет доли градуса. Поскольку вращающиеся объекты реагируют перемещением на 90 градусов от приложенной силы для правых (по часовой стрелке) вращающихся пуль, ось симметрии пули указывает вправо и немного вверх по отношению к направлению вектора скорости, когда снаряд вращается через его баллистическая дуга на дальней траектории.В результате этого небольшого наклона возникает непрерывный воздушный поток, который имеет тенденцию отклонять пулю вправо. Таким образом, возникновение рыскания покоя является причиной сноса пули вправо (при правосторонней закрутке) или влево (при левосторонней закрутке). Это означает, что пуля в любой данный момент «скользит» вбок и, таким образом, испытывает боковой компонент. [29] [30]
Следующие переменные влияют на величину гироскопического дрейфа:
- Длина снаряда или пули: более длинные снаряды подвержены большему гироскопическому сносу, поскольку они создают большую боковую «подъемную силу» при заданном угле рыскания.
- Скорость вращения: более высокая скорость вращения приводит к большему гироскопическому сносу, потому что нос в конечном итоге направлен дальше в сторону.
- Дальность, время полета и высота траектории: гироскопический дрейф увеличивается со всеми этими переменными.
- плотность атмосферы: более плотный воздух увеличивает гироскопический дрейф.
Результаты измерения доплеровским радаром гироскопического дрейфа нескольких американских военных и других пуль с очень низким лобовым сопротивлением на расстоянии 1000 ярдов (914,4 м) выглядят следующим образом:
| Тип пули | Мяч М193 армии США | Специальный мяч армии США M118 | Пальма-Сьерра MatchKing | Спичка LRBT J40 | Сьерра MatchKing | Сьерра MatchKing | Спичка LRBT J40 | Спичка LRBT J40 |
|---|---|---|---|---|---|---|---|---|
| Масса снаряда (в гранах) | 55 гр | 173 гр | 155 гр | 190 гр | 220 гр | 300 гр | 350 гр | 419 гр |
| Диаметр снаряда (в дюймах и мм) | .223 дюйма / 5,56 мм | 0,308 дюйма / 7,62 мм | 0,308 дюйма / 7,62 мм | 0,308 дюйма / 7,62 мм | 0,308 дюйма / 7,62 мм | 0,338 дюйма / 8,59 мм | 0,375 дюйма / 9,53 мм | 0,408 дюйма / 10,36 мм |
| Гироскопический дрейф (в дюймах и мм) | 23,00 дюйма / 584 мм | 11,50 дюйма / 292 мм | 12,75 дюйма / 324 мм | 3,00 дюйма / 76 мм | 7,75 дюйма / 197 мм | 6,5 дюйма / 165 мм | 0.87 дюймов / 22 мм | 1,90 дюйма / 48 мм |
Из таблицы видно, что гироскопический дрейф довольно изменчив и четкой тенденции не наблюдается.
Эффект Магнуса[]
Эффект Магнуса. V представляет ветер, стрелка F представляет собой результирующую силу Магнуса в сторону более низкого давления.
Снаряды со стабилизированным вращением подвержены эффекту Магнуса, при котором вращение пули создает силу, действующую либо вверх, либо вниз, перпендикулярно боковому вектору ветра.В простом случае горизонтального ветра и правостороннего (по часовой стрелке) направления вращения разность давлений вокруг пули, вызванная эффектом Магнуса, вызывает нисходящую (ветер справа) или восходящую (ветер слева) силу, если смотреть с точки стрельбы воздействовать на снаряд, влияя на его точку попадания. [31] Величина вертикального отклонения имеет тенденцию быть небольшой по сравнению с горизонтальной составляющей отклонения, вызванной ветром, но, тем не менее, может быть значительной при ветре, превышающем 4 м/с (14.4 км/ч или 9 миль/ч).
Эффект Магнуса и устойчивость пули[]
Эффект Магнуса играет важную роль в стабильности пули, потому что сила Магнуса действует не на центр тяжести пули, а на центр давления, влияющий на рыскание пули. Эффект Магнуса будет действовать как дестабилизирующая сила на любую пулю с центром давления, расположенным на впереди центра тяжести, и, наоборот, как стабилизирующая сила на любую пулю с центром давления, расположенным на позади центр тяжести.Расположение центра давления зависит от структуры поля течения, другими словами, в зависимости от того, находится ли пуля в сверхзвуковом, околозвуковом или дозвуковом полете. Что это означает на практике, зависит от формы и других характеристик пули, в любом случае сила Магнуса сильно влияет на стабильность, поскольку она пытается «закрутить» пулю на траектории полета. [32] [33]
Как это ни парадоксально, пули с очень низким лобовым сопротивлением из-за их длины имеют тенденцию демонстрировать большие дестабилизирующие ошибки Магнуса, потому что они имеют большую площадь поверхности, которую они представляют встречному воздуху, через который они летят. , тем самым снижая их аэродинамическую эффективность.Этот едва заметный эффект является одной из причин, по которой рассчитанное значение C d или BC, основанное на форме и плотности поперечного сечения, имеет ограниченное применение.
Эффект Пуассона[]
Еще одной незначительной причиной дрейфа, которая зависит от того, что носовая часть снаряда находится выше траектории, является эффект Пуассона. Это, если оно вообще происходит, действует в том же направлении, что и гироскопический дрейф, и даже менее важно, чем эффект Магнуса. Предполагается, что из-за запрокинутого носа снаряда под ним образуется воздушная подушка.Кроме того, предполагается, что между этой подушкой и снарядом увеличивается трение, так что последний при своем вращении будет стремиться скатиться с подушки и сместиться вбок.
Это простое объяснение довольно популярно. Однако нет доказательств того, что повышенное давление означает повышенное трение, и если это не так, не может быть никакого эффекта. Если он и существует, то должен быть весьма незначительным по сравнению с гироскопическим и кориолисовым дрейфом.
Эффекты Пуассона и Магнуса изменят направление дрейфа, если нос опустится ниже траектории.Когда нос смещен в одну сторону, как при равновесном рыскании, эти эффекты будут незначительно изменять дальность полета.
Дрейф Кориолиса[]
Дрейф Кориолиса вызван эффектом Кориолиса и эффектом Этвеша. Эти эффекты вызывают дрейф, связанный с вращением Земли, известный как дрейф Кориолиса. Кориолисов дрейф может быть вверх, вниз, влево или вправо. Кориолисов дрейф не является аэродинамическим эффектом; это следствие перелета из одной точки в другую по поверхности вращающейся планеты (Земли).
Направление дрейфа Кориолиса зависит от местоположения или широты стреляющего и цели на планете Земля и азимута стрельбы. Величина дрейфа зависит от места стрельбы и цели, азимута и времени полета.
Эффект Кориолиса[]
Эффект Кориолиса вызывает незначительные изменения траектории, вызванные вращением системы отсчета. Система координат, которая используется для указания местоположения точки стрельбы и местоположения цели, представляет собой систему широт и долгот, которая по сути является вращающейся системой координат, поскольку планета Земля представляет собой вращающуюся сферу.Во время своего полета снаряд движется прямолинейно (не считая пока гравитации и сопротивления воздуха). Поскольку цель вращается вместе с Землей, она фактически является движущейся целью относительно снаряда, поэтому, чтобы поразить ее, орудие должно быть направлено в точку, в которую снаряд и цель прилетят одновременно. Когда прямой путь снаряда отображается в используемой вращающейся системе координат, этот путь выглядит как криволинейный. Необходимо учитывать, что система координат вращается, а это достигается добавлением в уравнения движения членов для «центробежной силы» и «эффекта Кориолиса».Когда соответствующий член Кориолиса добавляется к уравнению движения, прогнозируемый путь относительно вращающейся системы координат становится криволинейным, что соответствует фактическому прямолинейному движению снаряда. Для наблюдателя с его системой отсчета в северном полушарии Кориолис создает впечатление, что снаряд изгибается вправо. На самом деле не снаряд, качающийся вправо, а земля (система отсчета), вращающаяся влево, приводит к такому результату. В южном полушарии, похоже, произойдет обратное.
Эффект Кориолиса максимален на полюсах и пренебрежимо мал на экваторе Земли. Причина этого в том, что эффект Кориолиса зависит от вектора угловой скорости вращения Земли относительно xyz — системы координат (системы отсчета). [34]
Для стрелкового оружия эффект Кориолиса, как правило, незначителен, но для баллистических снарядов с большим временем полета, таких как дальнобойные винтовочные снаряды, артиллерийские снаряды и межконтинентальные баллистические ракеты, он является существенным фактором при расчете траектория.
Эффект Этвёша[]
Эффект Этвеша изменяет кажущееся гравитационное притяжение движущегося объекта на основе взаимосвязи между направлением движения и направлением вращения Земли. Это вызывает тонкие изменения траектории.
Это не аэродинамический эффект и зависит от широты, будучи наиболее значительным на экваториальной широте. Объекты, движущиеся на восток, будут отклоняться вверх (ощущаться легче), а объекты, движущиеся на запад, будут отклоняться вниз (ощущаться тяжелее).Кроме того, объекты, движущиеся вверх или вниз, будут отклоняться соответственно на запад или восток. Принцип, лежащий в основе этих нелогичных изменений во время полета, более подробно объясняется в статье о принципе эквивалентности, посвященной физике общей теории относительности.
Для стрелкового оружия эффект Этвеша, как правило, незначителен, но для баллистических снарядов большой дальности с большим временем полета он может стать существенным фактором при точном расчете траектории.
Факторы снаряжения[]
Хотя это и не силы, действующие на траектории снарядов, существуют некоторые факторы, связанные с оборудованием, которые влияют на траектории. Поскольку эти факторы могут вызывать необъяснимое иначе внешнее баллистическое поведение в полете, их следует кратко упомянуть.
Боковой прыжок[]
Боковой прыжок вызван небольшим боковым и вращательным движением ствола орудия в момент выстрела. Это имеет эффект небольшой ошибки пеленга. Эффект игнорируется, так как он мал и меняется от раунда к раунду.
Боковой сброс[]
Боковое отбрасывание вызвано дисбалансом массы применяемых снарядов со стабилизацией вращения или дисбалансом давления на переходной фазе полета, когда снаряд вылетает из ствола орудия. Если он присутствует, он вызывает дисперсию. Эффект непредсказуем, так как он, как правило, невелик и варьируется от снаряда к снаряду, от снаряда к патрону и/или от ствола орудия к стволу орудия.
Максимальная эффективная дальность стрельбы из стрелкового оружия[]
Максимальная практическая дальность [примечание 4] всех видов стрелкового оружия и особенно мощных снайперских винтовок зависит, главным образом, от аэродинамической или баллистической эффективности используемых снарядов со стабилизацией вращения.Стрелки на дальние дистанции также должны собирать соответствующую информацию для расчета поправок на высоту и ветер, чтобы иметь возможность нанести первый выстрел по точечным целям. Данные для расчета этих поправок управления огнем имеют длинный список переменных, включая: [35]
- Баллистический коэффициент или полученные в результате испытаний коэффициенты аэродинамического сопротивления (Cd)/поведение используемых пуль
- высота прицельных элементов над осью канала ствола винтовки
- нулевая дальность, на которой производилась пристрелка прицельных компонентов и винтовочной комбинации в
- вес пули
- фактическая начальная скорость (температура пороха влияет на начальную скорость, воспламенение капсюля также зависит от температуры) Диапазон
- до цели
- сверхзвуковая дальность применяемой комбинации пистолета, патрона и пули
- угол наклона при стрельбе вверх/вниз
- целевая скорость и направление
- скорость и направление ветра (основная причина горизонтального отклонения снаряда и, как правило, самая сложная баллистическая переменная для правильного измерения и оценки.Воздействие ветра также может вызвать вертикальное отклонение.)
- колебания атмосферного давления, температуры, высоты над уровнем моря и влажности (от которых зависит плотность окружающего воздуха)
- Земная гравитация (незначительно меняется в зависимости от широты и высоты)
- гироскопический дрейф (гироскопический эффект в горизонтальной и вертикальной плоскостях, часто известный как дрейф вращения, вызываемый направлением и скоростью закручивания ствола)
- Дрейф эффекта Кориолиса (широта, направление стрельбы и данные северного или южного полушария определяют этот эффект)
- Эффект Этвеша (взаимосвязан с эффектом Кориолиса, широта и направление огня определяют этот эффект)
- боковой выброс (рассеивание, вызванное дисбалансом масс применяемого снаряда)
- аэродинамический прыжок (рассеивание, вызванное боковыми (ветровыми) импульсами, активируемыми во время свободного полета у дульного среза или очень близко к нему) [36]
- присущая потенциальная точность и диапазон регулировки прицельных компонентов
- присущая винтовке потенциальная точность
- присущая потенциальная точность боеприпаса
- присущая потенциальная точность компьютерной программы и других компонентов управления стрельбой, используемых для расчета траектории
Плотность окружающего воздуха максимальна в условиях арктического уровня моря.Холодный порох также создает более низкое давление и, следовательно, более низкую дульную скорость, чем теплый порох. Это означает, что максимальная практическая дальность стрельбы винтовок будет наименьшей в условиях арктического уровня моря.
Способность поразить точечную цель на большом расстоянии во многом зависит от способности справляться с экологическими и метеорологическими факторами, а также от хорошего понимания внешней баллистики и ограничений оборудования. Без (компьютерной) поддержки и высокоточных лазерных дальномеров и метеорологического измерительного оборудования в качестве вспомогательных средств для определения баллистических решений стрельба на дальние дистанции более 1000 м (1100 ярдов) на неизвестных дистанциях становится догадкой даже для самых опытных стрелков. [примечание 5]
Интересное дополнительное чтение: Wikibook по меткой стрельбе
Использование баллистических данных[]
Вот пример баллистической таблицы для матчевой пули Speer 169 гран (11 г) калибра .30 с остроконечным хвостом и БК 0,480. Предполагается, что прицелы расположены на 1,5 дюйма (38 мм) выше линии ствола, а прицелы отрегулированы таким образом, чтобы точка прицеливания и точка попадания совпадали на расстоянии 200 ярдов (183 м) и 300 ярдов (274 м) соответственно.
| Диапазон | 0 | 100 ярдов (91 м) | 200 ярдов (183 м) | 300 ярдов (274 м) | 400 ярдов (366 м) | 500 ярдов (457 м) | |
|---|---|---|---|---|---|---|---|
| Скорость | фут/с | 2700 | 2512 | 2331 | 2158 | 1992 | 1834 |
| м/с | 823 | 766 | 710 | 658 | 607 | 559 | |
| Пристрелян на 200 ярдов (184 м) | |||||||
| Высота | в | -1.5 | 2,0 | 0 | -8,4 | -24,3 | -49,0 |
| мм | -38 | 51 | 0 | -213 | -617 | -1245 | |
| Пристрелян на 300 ярдов (274 м) | |||||||
| Высота | в | -1,5 | 4,8 | 5,6 | 0 | -13,1 | -35,0 |
| мм | -38 | 122 | 142 | 0 | -333 | -889 | |
Эта таблица показывает, что даже при достаточно аэродинамической пуле, выпущенной с высокой скоростью, «падение пули» или изменение точки попадания является значительным.Это изменение точки удара имеет два важных следствия. Во-первых, оценка расстояния до цели имеет решающее значение на больших дальностях, потому что разница в точке попадания между 400 и 500 ярдами (460 м) составляет 25–32 дюйма (в зависимости от нуля), другими словами, если стрелок оценивает, что цель находится на расстоянии 400 ярдов, когда на самом деле она находится на расстоянии 500 ярдов, выстрел попадет на 25–32 дюйма (635–813 мм) ниже места прицеливания, возможно, полностью не попав в цель. Во-вторых, винтовку следует пристрелять на расстояние, соответствующее типичному диапазону мишеней, потому что стрелку, возможно, придется целиться так высоко над мишенью, чтобы компенсировать большое падение пули, что он может полностью потерять мишень из виду (например, вне поля зрения оптического прицела).В примере с винтовкой, пристрелянной на расстоянии 200 ярдов (180 м), стрелок должен будет прицелиться на высоте 49 дюймов или более 4 футов (1,2 м) над точкой попадания для цели на расстоянии 500 ярдов.
Бесплатное программное обеспечение для внешней баллистики стрелкового оружия[]
- Баллистический_XLR. (таблица MS Excel)] — существенное улучшение и модификация электронной таблицы Pejsa (ниже).
- GNU Exterior Ballistics Computer (GEBC) — баллистический компьютер 3DOF с открытым исходным кодом для Windows, Linux и Mac — поддерживает модели сопротивления G1, G2, G5, G6, G7 и G8.Создан и поддерживается Дереком Йейтсом.
- Баллистический раздел 6mmbr.com содержит ссылки на 4 бесплатные внешние баллистические компьютерные программы.
- 2DOF и 3DOF RL McCoy — внешняя баллистика Gavre (zip-файл) — поддерживает модели сопротивления G1, G2, G5, G6, G7, G8, GS, GL, GI, GB и RA4
- PointBlank Ballistics (zip-файл) — драг-модель Siacci/Mayevski G1.
- Ремингтон Стреляй! Баллистический калькулятор для заводских боеприпасов Remington (на основе программного обеспечения Pinsoft Shoot!).- Дрэг-модель Siacci/Mayevski G1.
- Калькуляторы баллистики для стрелкового оружия JBM Онлайн-калькуляторы траектории — поддерживает G1, G2, G5, G6, G7 (для некоторых снарядов экспериментально измерены баллистические коэффициенты G7), G8, GI, GL и для некоторых снарядов, полученных в результате доплеровского радиолокационного теста (C d ) дрэг-модели. [37]
- Баллистика Пейса (таблица MS Excel) — модель Пейса.
- Друг-стрелок (ПО Palm PDA) — модель Пейса.
- Quick Target Unlimited, Lapua Edition — версия баллистического программного обеспечения QuickTARGET Unlimited (для загрузки требуется бесплатная регистрация) — поддерживает G1, G2, G5, G6, G7, G8, GL, GS Spherical 9/16″ SAAMI, GS Spherical Don Миллер, RA4, советский блокнот 1943 г., британский блокнот люков 1909 г. и для некоторых моделей сопротивления снарядов Lapua, полученных на основе доплеровских радиолокационных испытаний (Cd).
- Lapua Ballistics Exterior баллистическая программа для мобильных телефонов Java или Android. Основано на моделях сопротивления снарядов и патронов Lapua, полученных в результате испытаний доплеровского радара (Cd).
- BfX — Ballistics for Excel Набор надстроек для MS Excel. Поддерживает модели G1, G2, G5, G6, G7, G8, RA4 и Pejsa, а также одну для пуль для пневматической винтовки. Возможность обработки пользовательских моделей, например. Снаряды Lapua доплеровского радиолокационного происхождения (Cd).
- GunSim «GunSim» — бесплатная браузерная программа-симулятор баллистики для Windows и Mac.
- BallisticSimulator «Баллистический симулятор» — бесплатная программа-симулятор баллистики для Windows.
- ChairGun Pro Free Ballistics для кольцевого и пневматического ружья.
- 5H0T Бесплатный баллистический онлайн-калькулятор с возможностью экспорта данных и построения графиков.
См. также[]
- Внутренняя баллистика — поведение снаряда и пороха до того, как он покинет ствол.
- Переходная баллистика — поведение снаряда с момента его вылета из дульного среза до момента выравнивания давления за снарядом.
- Терминальная баллистика — Поведение снаряда при ударе о цель.
- Траектория снаряда — Основные математические формулы внешней баллистики.
- Правило стрелка — Процедуры или «правила» для стрелка при прицеливании по целям на расстоянии вверх или вниз по склону.
Примечания[]
- ↑ Большинство снарядов со стабилизированным вращением, которые страдают от недостаточной динамической устойчивости, имеют проблему вблизи скорости звука, когда аэродинамические силы и моменты претерпевают большие изменения.Менее распространено (но возможно) то, что пули демонстрируют значительное отсутствие динамической стабильности на сверхзвуковых скоростях. Поскольку динамическая устойчивость в основном определяется околозвуковой аэродинамикой, очень сложно предсказать, когда снаряд будет иметь достаточную динамическую устойчивость (это аэродинамические коэффициенты, которые труднее всего точно рассчитать в наиболее трудно предсказуемом скоростном режиме (трансзвуковой)). Аэродинамические коэффициенты, определяющие динамическую устойчивость: момент тангажа, момент Магнуса и сумма коэффициентов динамического момента по тангажу и углу атаки (величина, которую очень сложно предсказать).В конце концов, моделирование и симуляция мало что могут сделать для точного прогнозирования уровня динамической стабильности пули на дальности полета вниз. Если пуля имеет очень высокий или низкий уровень динамической стабильности, моделирование может дать правильный ответ. Однако, если ситуация является пограничной (динамическая устойчивость около 0 или 2), нельзя полагаться на моделирование для получения правильного ответа. Это одна из тех вещей, которые должны быть проверены в полевых условиях и тщательно задокументированы.
- ↑ G1, G7 и доплеровские радиолокационные испытания, полученные в результате испытаний коэффициентов аэродинамического сопротивления (C d ), предсказания метода прогнозирования, рассчитанные с помощью QuickTARGET Unlimited, Lapua Edition.Прогнозы Pejsa, рассчитанные с помощью баллистического программного обеспечения Lex Talus Corporation Pejsa с постоянным коэффициентом наклона, установленным на значение по умолчанию 0,5.
- ↑ Данные C d используются инженерами для создания алгоритмов, которые используют как известные математические баллистические модели, так и тестовые табличные данные в унисон для получения прогнозов, которые очень близки к фактическому поведению в полете.
- ↑ Веб-сайт snipershide определяет эффективную дальность как: дальность, в которой компетентный и обученный человек, использующий огнестрельное оружие, может поразить цель в шестидесяти-восьмидесяти процентах случаев.На самом деле у большинства огнестрельного оружия истинная дальность намного больше, чем эта, но вероятность поражения цели невелика на дальности, превышающей эффективную. Кажется, не существует хорошей формулы для эффективной дальности стрельбы из различного огнестрельного оружия.
- ↑ Пример того, насколько точно стрелок на дальние дистанции должен установить параметры прицеливания для расчета правильного баллистического решения, объясняется этими результатами пробной стрельбы. Винтовка .338 Lapua Magnum, прицеленная на расстоянии 300 м, стреляла пулями Lapua Scenar весом 250 гран (16,2 г) с измеренной начальной скоростью 905 м / с.Плотность воздуха ρ во время пробной стрельбы составила 1,2588 кг/м³. Испытательной винтовке потребовалась коррекция возвышения 13,2 мил (45,38 МОА) с нулевой дальности 300 м на 61 градусе широты (гравитация незначительно меняется в зависимости от широты), чтобы поразить цель размером с торс человека в мертвой точке на 1400 м. График баллистической кривой показал, что между 1392 и 1408 м пули должны были поразить цель высотой 60 см (2 фута). Это означает, что если бы была допущена ошибка дальности всего 0,6%, цель высотой 60 см на высоте 1400 м была бы полностью пропущена.Когда та же цель была установлена на менее сложной дистанции 1000 м, ее можно было поразить на расстоянии от 987 м до 1013 м, а это означает, что погрешность определения дальности 1,3% будет вполне приемлемой для возможности поразить цель высотой 2 МОА из .338 Lapua. Снайперский патрон Магнум. Это делает очевидным, что с увеличением расстояния кажущиеся незначительными ошибки измерения и оценки становятся серьезной проблемой.
Ссылки[]
- ↑ Баллистических коэффициентов не существует! Рэнди Уэйкман
- ↑ Weite Schüsse — drei (нем.)
- ↑ Историческая справка
- ↑ Пули класса LM, пули с очень высоким БК для дальних дистанций в ветреную погоду.
- ↑ Улучшенный баллистический коэффициент
- ↑ .Брошюра о модели 338 Lapua Magnum от Lapua
- ↑ 300 гр Брошюра Scenar HPBT от Lapua
- ↑ Баллистические коэффициенты — объяснение
- ↑ Form Factors: A Useful Analysis Tool Брайан Литц, главный баллист Berger Bullets
- ↑ http://www.pejsa.com/ Баллистика Пейса
- ↑ Артур Дж. Пейса (2002). Справочник Пейсы по новой прецизионной баллистике . Издательство Кенвуд. п. 3.
- ↑ 12,0 12,1 Артур Дж. Пейса (2008). Новая точная баллистика стрелкового оружия . Издательство Кенвуд. стр. 65–76.
- ↑ Артур Дж. Пейса (2008). Новая точная баллистика стрелкового оружия . Издательство Кенвуд. п. 63.
- ↑ Артур Дж. Пейса (2002). Справочник Пейсы по новой прецизионной баллистике . Издательство Кенвуд. п. 34.
- ↑ Артур Дж. Пейса (2002). Справочник Пейсы по новой прецизионной баллистике . Издательство Кенвуд. п. 4.
- ↑ Артур Дж. Пейса (2008). Новая точная баллистика стрелкового оружия .Издательство Кенвуд. стр. 131–134.
- ↑ Функции перетаскивания Ballistics for Excel
- ↑ Артур Дж. Пейса (2008). Новая точная баллистика стрелкового оружия . Издательство Кенвуд. стр. 33–35.
- ↑ Баллистическое программное обеспечение на базе Lex Talus Corporation Pejsa
- ↑ Баллистическое программное обеспечение на базе Patagonia Ballistics Pejsa
- ↑ Чак Хоукс. «8x50R Лебель (8 мм Лебель)» . http://www.chuckhawks.com/8mm_lebel.htm.
- ↑ Прототип самонаводящейся пули Sandia может поразить цель на расстоянии мили
- ↑ Данные коэффициента перетаскивания пуль Lapua для QuickTARGET Unlimited
- ↑ Данные компакт-диска с пулями Lapua (zip-файл)
- ↑ QuickTARGET Unlimited, издание Лапуа
- ↑ Бесплатное программное обеспечение внешней баллистики Lapua Ballistics для мобильных телефонов
- ↑ ВЛИЯНИЕ НАРЕЗАЛЬНЫХ КАНАВОК НА ХАРАКТЕРИСТИКИ МАЛОКАЛИБЕРНЫХ БОЕПРИПАСОВ Sidra I.Силтон* и Пол Вайнахт Исследовательская лаборатория армии США Абердинский испытательный полигон, Мэриленд 21005-5066
- ↑ Наклонный огонь — 3 метода корректировки прицеливания — Уильям Т. Макдональд, июнь 2003 г.
- ↑ Нэнстиэль Йоу покоя
- ↑ Гироскопический (спиновый) дрейф и эффект Королиса Брайан Литц
- ↑ Ненстиэль Эффект Магнуса
- ↑ Ненстиэль Сила Магнуса
- ↑ Ненстиэль Момент Магнуса
- ↑ Гироскопический дрейф и ускорение Coreolis от Брайана Литца
- ↑ Исследовательская лаборатория армии США в 1999 году провела исследование практических ограничений нескольких систем снайперского оружия и различных методов управления огнем.Анализ бюджета ошибок управления огнем снайперского оружия — Раймонд фон Вальде, Деннис Мец, август 1999 г.
- ↑ Эффекты аэродинамического прыжка, вызванного равномерной последовательностью боковых импульсов — Джин Р. Купер, июль 2004 г.
- ↑ JBM Bullet Library
Внешние ссылки[]
Общая внешняя баллистика
Внешняя баллистика стрелкового оружия
Артиллерийская внешняя баллистика
Основы баллистики
Основы баллистикиОсновы баллистики
Как стрелки, мы все заинтересованы в том, куда летит пуля после выстрела.Способность поместить пулю туда, куда мы хотим, жизненно важна для любого точного стрелка, и понимание баллистики необходимо для последовательного и надежного выполнения этой задачи. Совокупность знаний о факторах, влияющих на полет пули с момента вылета из дульного среза ружья до момента попадания в цель, называется внешней баллистикой, и это предмет нашего обсуждения.Чтобы убедиться, что мы все говорим на одном языке, приведем некоторые определения терминов.Это будет проще сделать, если обратиться к схеме полета круглого шара, созданной баллистической программой Gun Controller® от Recreational Software, Inc. (RSI).
Линия прицеливания: Совершенно прямая линия от глаза стрелка через целик, затем мушку, затем цель. На графике линия видимости начинается с «0» и представляет собой черную линию, проходящую прямо через график в центре заштрихованной синей области. Очевидно, что когда стрелок наводит пистолет, он смотрит по линии прицеливания.
Линия канала ствола: Прямая линия, проходящая по центру канала ствола ружья. Как мы увидим, это не совпадает с линией обзора.
Истинное падение: Истинное падение, показанное синей линией на графике, представляет собой фактическое расстояние, на которое пуля падает во время полета до цели. Важно понимать, что это не то же самое, о чем мы говорим, когда обсуждаем падение в обычном смысле, которое правильнее называть фактическим или кажущимся падением.Простой способ представить это таков: держите в руке круглый шар, совершенно идентичный тому, в который стреляют, точно на том же уровне над землей; сделайте линию ствола ружья точно параллельной земле; выстрелить из ружья, и в тот самый момент, когда пуля вылетит из дула, выроните пулю из рук. Мяч, выпущенный из ружья, и тот, что выброшен из вашей руки, ударятся о землю в одно и то же мгновение, один у ваших ног, а другой на расстоянии многих ярдов дальше. Поскольку два одинаковых мяча, брошенные с одной и той же высоты, ударились о землю в одно и то же время, они должны падать с одинаковой скоростью.Это верно, потому что оба шара, как и все остальное на земле, подвержены ускорению свободного падения, которое постоянно при любых обстоятельствах. Что бы мы ни делали, мяч «падает» все время, пока он находится в полете, даже когда он движется вверх.
Путь: Красная линия на диаграмме показывает то, что нас очень интересует, а именно реальный путь пули в воздухе после того, как она вылетела из дульного среза. На окончательную форму этого пути влияет множество факторов, некоторые из которых мы обсудим.
Это тот факт, что True Drop является постоянным и неизбежным, вокруг которого вращается все остальное в базовой баллистике. Чтобы проиллюстрировать это, эта диаграмма была подготовлена с использованием круглого шара 0,600, движущегося со скоростью 1247 футов/сек. Мяч весит 324,3 грана, ружье пристреляно на 75 ярдов, стрельба велась в стандартных атмосферных условиях на уровне моря (температура 59°F, барометрическое давление 29,53 дюйма ртутного столба, относительная влажность 78%). График представляет собой лишь гипотетическую ситуацию.
Данные, использованные для создания диаграммы, показывают, что True Drop на 75 ярдах составляет 7,55 дюйма. Это означает, что если мы направим ствол, линию ствола, прямо на цель, шар попадет на 7,55 дюйма ниже. Каждый раз, и мы не можем этого изменить. Итак, обманываем, очень простым способом. Мы направляем ствол выше цели ровно настолько, чтобы компенсировать падение на 7,55 дюйма. Затем мы настраиваем прицел пушки так, чтобы линия обзора указывала прямо на цель, и забываем об этом. Теперь легко увидеть разницу между True Drop и Apparent Drop….Мы знаем, что мяч на самом деле падает с высоты 7,55 дюйма, но поскольку он попадает в цель, когда мы наводим на нее цель, кажущееся падение равно нулю на целевом расстоянии.
Из этой установки следует несколько вещей. Мы знаем, что линия ствола находится ниже линии прицеливания на дульном срезе, потому что прицельные приспособления находятся на верхней части ствола. (Для среднего дульнозарядного устройства это расстояние составляет 0,85 дюйма.) Поскольку линия ствола, то есть ствол, направлена вверх, чтобы «закинуть» пулю в цель, линия ствола должна пересекать линию прицеливания, идя вперед. вверх.Мяч, который стартует вдоль линии ствола, быстро падает ниже нее, но не раньше, чем пересекает линию видимости. В зависимости от орудия, скорости и дальности прицеливания это происходит на расстоянии от 5 до 10 ярдов перед дульным срезом. Место, где пуля пересекает линию прямой видимости в первый раз, направляясь вверх, на графике называется Near Zero Range , NZ. Пуля движется дальше, достигая максимальной высоты над линией обзора, а затем начинает падать. Точка, в которой достигается этот максимум над линией прямой видимости, на графике называется Mid-Range Trajection , MRT.Это происходит, как правило, на расстоянии более 50 процентов от мишени. Продолжая движение, пуля падает ближе к линии прицеливания, пока снова не пересекает ее на целевой дистанции, дальности дальнего нуля .
Теперь у нас есть изображение Пути от дула до цели… ниже линии визирования у дула, пересекает линию визирования близко к дулу в ближнем нуле, достигает максимальной высоты над линией визирования в середине. -Диапазон траектории, остается над линией обзора до тех пор, пока снова не пересечет ее в целевой дальности, Far Zero.
При рассмотрении внешней баллистики на самом базовом уровне обсуждения необходимо обсудить еще один аспект проблемы, а именно форму этой красивой красной линии на графике. Идеальный Путь точно совпадал бы с Линией Визирования, и увидеть цель означало бы поразить ее. Извините, этого никогда не будет. Очевидно, что разные пули, выпущенные с разной скоростью, будут вести себя по-разному. Основным фактором, определяющим форму траектории, является скорость, с которой пуля любой формы замедляется.Поскольку Истинное Падение является постоянной величиной, происходящей с постоянно увеличивающейся скоростью, мы можем видеть, что если пуля летит очень быстро, она пролетит большое расстояние по дальности за любую заданную единицу времени и за определенное количество Истинного Падения. Если он движется медленно, он пройдет гораздо меньшее расстояние вниз за ту же единицу времени, но упадет ровно на ту же величину. Таким образом, форма Пути в начале довольно плоская, но по мере приближения к цели все больше и больше изгибается, потому что пуля замедляется.Форма всех траекторий подобна параболе с постоянно увеличивающейся степенью кривизны.
Почему одна пуля замедляется быстрее другой? Проще говоря, потому что у него больше сопротивления (больше трения в воздухе) или меньше инерции. Почему у человека сопротивление больше? Из-за разницы в форме, которая создает большее трение. Обтекаемая пуля режет воздух легче, чем тупая, неправильной формы. Таким образом, пуля, разработанная для современной высокоскоростной винтовки и выпущенная из нее, будет иметь гораздо меньшее сопротивление, чем коническая или круглая пуля, выпущенная из порохового ружья.Инерция — это свойство, которое заставляет любое движущееся тело двигаться в том же направлении и с той же скоростью, если на него не действует какая-то внешняя сила. Инерция увеличивается за счет увеличения массы (думаю, веса) и скорости. На нашу летящую пулю действуют две внешние силы: гравитация заставляет ее падать, а трение о воздух заставляет ее замедляться.
Становится очевидным, что более тяжелые пули и более обтекаемые пули сопротивляются замедлению лучше всего.
Чтобы иметь возможность сравнивать эффективность различных пуль, был разработан математический инструмент, который называется баллистическим коэффициентом (BC) .Это может понравиться только математику, но на самом деле это очень просто. Пуля заданной формы (форма не имеет значения) и веса была выпущена тысячи раз, и ее лобовое сопротивление, скорость ее замедления были точно определены. Это было названо стандартной пулей. Теперь, чтобы сравнить производительность нашего любимого снаряда, все, что нам нужно сделать, это сравнить скорость его замедления со скоростью стандартной пули. Если она замедляется точно так же, как и стандартная пуля, говорят, что ее баллистический коэффициент равен 1.0. Любой БК ниже 1,0 указывает на то, что пуля не так хорошо пробивает воздух и сохраняет свою скорость, как стандартная пуля. Те из нас, кто интересуется стрельбой черным порохом и баллистикой наших пуль, быстро узнают, что БК круглой пули ниже, чем у конической, и что обе они намного ниже, чем у стандартной пули. Поскольку круглый шар… круглый шар…, его форму нельзя изменить. Чтобы компенсировать низкий БК, мы можем сделать две вещи, увеличить вес, потому что более тяжелый снаряд имеет большую инерцию и больше сопротивляется замедлению, и стартовать с большей начальной скоростью, чтобы скорость у цели была выше, даже после всех потерь .
Тома были написаны о внешней баллистике, и это обсуждение едва касалось поверхности. Тем не менее, если вы уделили пристальное внимание, нет никаких причин, по которым ваши цели не должны выглядеть так.
© 1997 Б.Е. Спенсер
Вернуться к записной книжке
Мини-шар и его параболическая траектория
Мяч Минье, пуля, которую чаще всего называют оружием массового поражения в гражданской войне, носит имя капитана французской армии Клода-Этьена Минье.Ему обычно приписывают решение проблемы использования расширяющихся газов, чтобы заставить части пули попасть в канавки винтовки. Другие улучшили его дизайн.
. Источник: http://wigwags.wordpress.com/category/history-associations/the-american-civil-war/. . Эти кольца выполняли две задачи: во-первых, минимизировать трение в канале ствола винтовочного мушкета, а во-вторых, обеспечивать наведение во время полета.Цилиндрическая форма — это отход от предыдущей мушкетной пули — шаровой. Такая форма позволяла мини-шару выходить из канала ствола винтовочного мушкета линейным образом. Конструкция основания позволяла газам, образующимся при взрыве 60 граммов пороха, заталкивать нижний конец пули в канавки винтовки для ее вращения. Это вращение имело тенденцию повышать точность пули, почти так же, как квотербек бросает футбольный мяч. Вторым элементом для улучшения наведения являются кольца.Это исправило любую склонность пули к раскачиванию в полете. Это было достигнуто за счет увеличения сопротивления воздушному потоку, если одна часть пули отклонялась влево или вправо по траектории полета пули. Пуля будет отброшена назад туда, где сопротивление воздуха будет минимальным. См. К. Уилкокс, с. 130-134 для более технических объяснений http://books.google.com/books/about/Rifles_and_Rifle_Practice.html?id=JNtEAAAAIAAJ
От этого новшества, использования колец, вскоре после гражданской войны отказались, так как оно существенно увеличивало сопротивление воздуха и способствовало уменьшению его дальности и формы траектории – параболической дуги.Мини-мяч из-за его относительно низкой начальной скорости был более заметен, чем дальше пытался выстрелить. Это природное явление связано с гравитацией. Сопротивление воздуха означает, что пуля летит медленнее, и гравитация притягивает ее вниз. Джек Коггинс в своей книге «Вооружение Гражданской войны» нарисовал траекторию пули следующим образом, уподобив ее радуге.
Точнее, хвостовая часть его полета имеет более выраженный нисходящий путь и, следовательно, короче. Из этой диаграммы видно, что опасное пространство, как назвал его Уилкокс, находится в начальной и конечной точках траектории полета пули.
Для меня это изменит то, что я назвал опасной зоной. Одной из первых четких моделей этого стал блог 67thtigers. http://67thtigers.blogspot.com/2010/05/ballistics.html.
Его рисунок, воспроизведенный ниже, демонстрирует высокую параболическую дугу мини-шара.
На этом графике земля выделена голубым цветом внизу. Фиолетовая горизонтальная линия представляет собой высоту макушки головы. Мушкетная винтовка нацелена на три разных дистанции; 100 ярдов, 300 ярдов и 500 ярдов.Они совпадают с тремя предустановленными прицельными отверстиями, предусмотренными на винтовочном мушкете Springfield. Высота в дюймах относительно дульного среза стрелка указана по левой оси. Легко оценить вызов солдату гражданской войны, поразившему цель. Док Уайт так описал проблему. http://www.whitemuzzleloading.com/long_range_muzzleloading.htm
«Стрельба по цели на расстоянии 225 ярдов из винтовки Springfield затруднена; вы должны установить прицел на 300 ярдов, а затем прицелиться ниже ног цели, что неудобно, когда плохо обученные солдаты, естественно, стреляют высоко.Решение, принятое для линейной пехоты США, CS, а также большей части континентальной Европы, заключалось в том, чтобы установить прицел на 100 ярдов и стрелять только на 150 ярдов или меньше».
Учитывая такое понимание проблемы параболической дуги, я искал программу, которая помогла бы мне в построении графика воздействия болота на солдаты как конфедератов, так и союзников во время битвы при Фредериксбурге в декабре 1862 года.
Мой следующий блог покажет результаты.
Нравится:
Нравится Загрузка…
РодственныеО Питере Глайере
Я на пенсии с пожизненным интересом к истории, в первую очередь Гражданской войны и Второй мировой войны — Европы. Я был армейским инженером, отсюда и мой интерес к местности. Я получил степень в области городского и регионального планирования и магистра в области международных отношений. Объяснение базовой траектории пули— Enfield-Rifles.com
Хорошее место для начала — прочитать следующую статью Wikihttp://en.wikipedia.org/wiki/Rifleman’s_rule
В самой простой форме вам необходимо знать следующее:
Линия прямой видимости (LOS)
Горизонтальное расстояние до цели
Траектория пули
цель, которая видна, через прицел, к цели. Его не следует путать с траекторией пули. На LOS не влияет гравитация, уклон и другие факторы окружающей среды. (Извините, ученый-квант.)
Траектория пули — это траектория движения пули на определенном расстоянии.Это не параллельно LOS, поскольку на пулю влияет гравитация, горизонтальное расстояние, кривая земли и вращение земли. Да, ветер, влажность, температура, плотность воздуха и т. д. тоже влияют на это. Но они, наряду с кривой Земли и вращением Земли, пока являются второстепенными факторами. Чтобы просто не сказать, что путь кривой. Как только пуля вылетает, ствол начинает опускаться ниже конца ствола. Форма и вес пули (BC и SD), скорость закручивания и скорость пули — все это влияет на скорость падения пули.Медленные и тяжелые пули падают быстрее, чем легкие и быстрые.
Для простоты этого поста я пока не буду учитывать факторы окружающей среды, т.е. ветер, плотность воздуха и т.д.
И еще есть горизонтальное расстояние до цели. Это не следует путать с расстоянием над землей до цели. Чем круче уклон, тем меньше горизонтальное расстояние по отношению к расстоянию над землей до цели. Допустим, вы стреляли по мишени вниз/вверх по склону под углом 45 градусов. Если бы вы увеличили темп, и это было бы 280 м, вы бы на самом деле стреляли только по цели, находящейся на расстоянии 200 м (теорема Пифагора).Это потому, что гравитация влияет только на горизонтальное расстояние.
Как это нам поможет? Чтобы прицелиться в огнестрельном оружии, нам нужно знать, где будет находиться пуля на заданном расстоянии. Знание того, что делает пуля в полете, ее траектория, поможет нам понять, где ожидать, что пуля окажется.
Траектория | Encyclopedia.com
шторм
просмотров обновлено 29 мая 2018Траектория пули — это траектория полета, по которой она следует от момента выстрела до достижения цели.В случаях стрельбы, целью которой является жертва, судебно-медицинский эксперт захочет попытаться определить траекторию пули в рамках реконструкции места преступления . Наука об исследовании движения снаряда известна как баллистика и включает в себя уравнения, которые можно использовать для расчета траектории.
При нажатии на спусковой крючок происходит взрыв оболочки пули. Химическая энергия преобразуется в кинетическую энергию, и пуля вылетает из пистолета с большой скоростью.В этот момент на него действуют силы гравитации и сопротивления воздуха, которые заставляют его двигаться примерно по параболической траектории. Дальность траектории — это общее расстояние, которое проходит пуля в горизонтальном направлении, то есть расстояние между пушкой и ее целью.
При анализе траектории пули баллисты делят ее на три части. Во-первых, это короткий путь, который совершает пуля от места удара бойка до места, где она покидает ружье.Затем он совершает путешествие к своей цели, которое может длиться от доли секунды до нескольких секунд. Наконец, пуля теряет свою кинетическую энергию при прохождении через цель. Пуля может застрять в теле жертвы или, если она имеет достаточную кинетическую энергию, может выйти с другой стороны, создав как выходное, так и входное ранение. Иногда пуля рикошетит, то есть отклоняется от своей траектории из-за столкновения с объектом. Он все еще может попасть в кого-то, но выстрел не будет направлен прямо на жертву, что может быть важной частью улики .
Основная задача специалиста по баллистике — определить диапазон траектории пули. Когда пуля вылетает из пистолета, она уносит с собой различные газы, которые часто образуют на коже жертвы рисунок, напоминающий татуировку. Масштабы и распространение этого паттерна часто показывают разницу между преступником и жертвой. Исследователь часто пытается воспроизвести картину, стреляя из оружия, если оно доступно, или из аналогичного оружия по пустым мишеням в лабораторной ситуации.Знание расстояния может помочь установить, где стоял преступник, и может либо опровергнуть, либо подтвердить показания свидетелей.
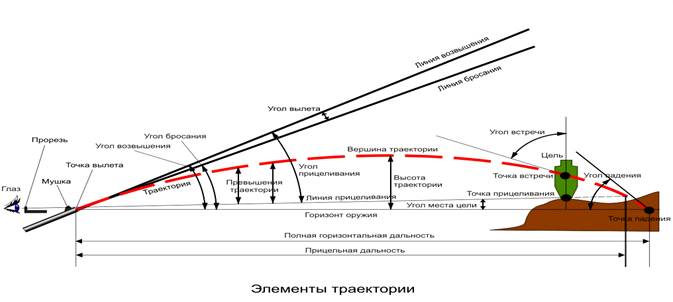
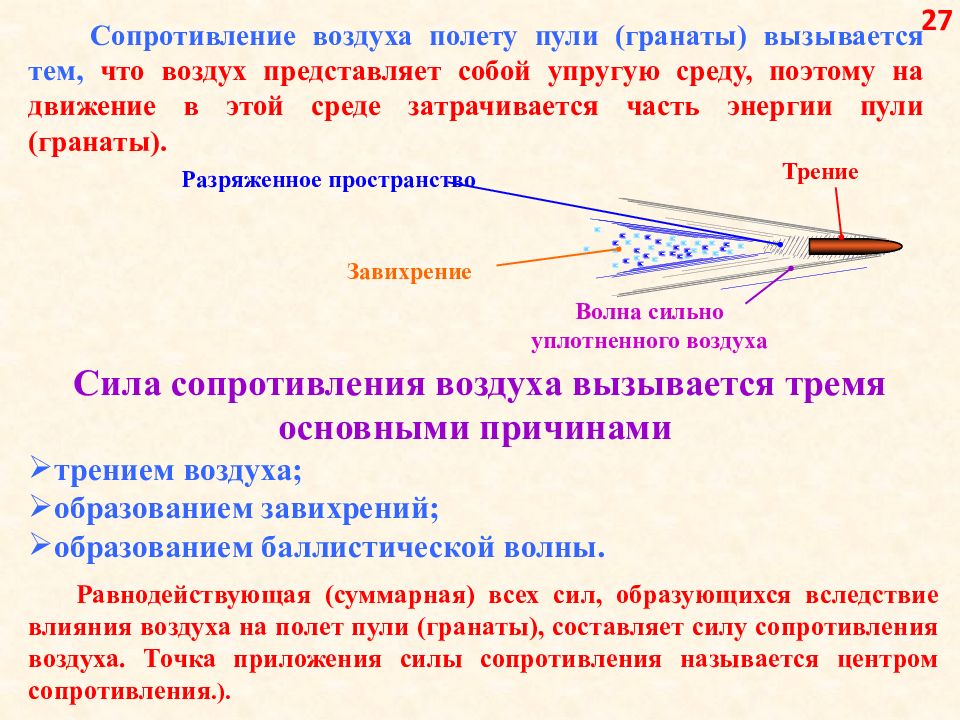
 9).
9).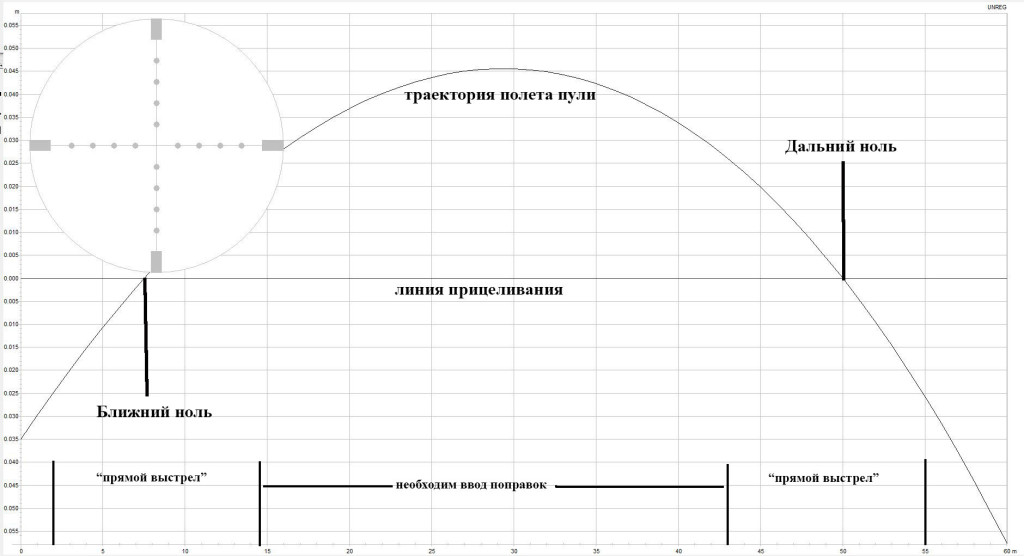
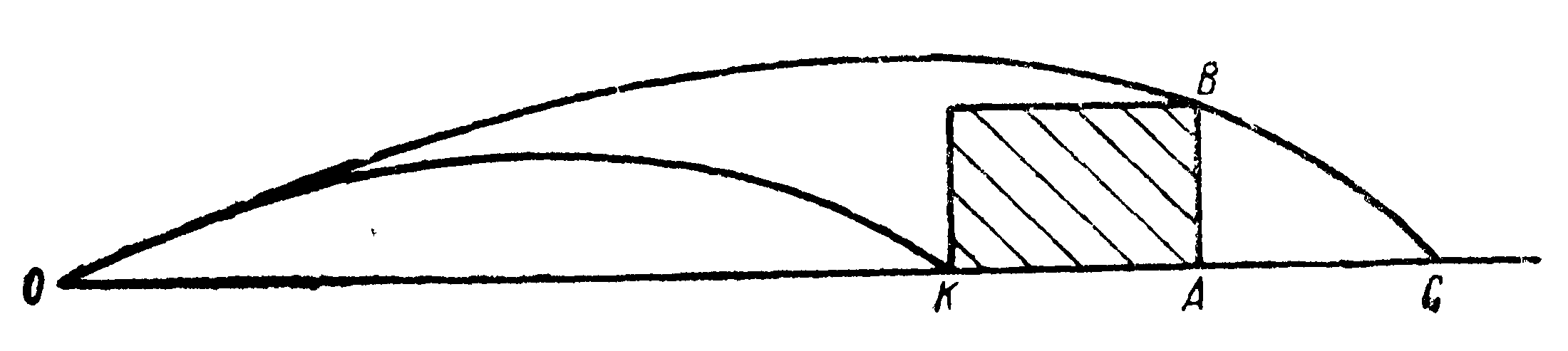 Для вычисления точного времени, прошедшего с момента предыдущего рендеринга, требуется больше логики.
Для вычисления точного времени, прошедшего с момента предыдущего рендеринга, требуется больше логики.