Виды дробей. Определения обыкновенной дроби, правильной дроби, неправильной дроби, смешанного числа и десятичной дроби.
Чтобы сто раз не повторяться мы решили сделать страницу о видах дробей, какие виды дробей бывают, как эти виды и типы дробей называются. Ну а темы, различных математический действий с этими дробями по ссылке сверху…Виды, типы дробей
Дроби делятся на десятичные.Какая дробь называется десятичной?
Записываются в строчку имеют вид обычного числа, но только в нём присутствует точка.До точки называется целое, после точки десятичная часть например:
15.1 – 15 целых одна десятая
15.25 – 15 целых 25 сотых
Какая дробь называется обычной?
Тип или вид обычных дробей в свою очередь делится на правильную и неправильную дробьКакая дробь называется правильная?
Правильная дробь – это когда числитель (верхняя часть дроби) меньше знаменателя.
Звучит правильная дробь так(например) — «одна вторая» и записывается так:
12
Какая дробь называется не правильная?
Не правильная дробь отличается от правильной тем, что числитель больше знаменателя.Записывается точно так же и звучит так же!
Неправленая дробь – например звучит «три вторых» и выглядит так:
32Смешанная дробь:
Какая дробь называется не смешанная?
Смешанная дробь получается при выделении целого числа из неправильной дроби. Из правильной дроби смешанную дробь сделать нельзя! Возьмем выше приведенную неправильную дробь и сделаем из неё смешанную. Звучит так : «одна целая одна вторая» — записывается впереди дроби пишется целое, за целым пишется дробь. Не будем повторяться – здесь мы уже один раз превращали неправильную дробь в смешанную. 32 => 112Написать что-нибудь.
 .. какие бывают дроби ,
какие бывают дроби в математике ,
какие виды дробей бывают,
какие бывают десятичные дроби ,
какие бывают неправильные дроби ,
какие бывают дроби в математике 6 класс ,
какие бывают дроби в математике 5 класс ,
какая бывает дробь для охоты, » />
.. какие бывают дроби ,
какие бывают дроби в математике ,
какие виды дробей бывают,
какие бывают десятичные дроби ,
какие бывают неправильные дроби ,
какие бывают дроби в математике 6 класс ,
какие бывают дроби в математике 5 класс ,
какая бывает дробь для охоты, » />Дроби, представление числа: обозначение, деление, виды. Правильные, неправильные, конечные, бесконечные
Тестирование онлайн
Определение дроби
Сейчас 3 апельсина разделим на 20 человек. Каждому достанется часть от того, что было.
Если взять два куска арбуза (предыдущая картинка), то получим дробь
На следующем рисунке изображена дробь (закрашенная часть)
Обозначение дроби
Обозначается дробь, как .
Черта «-» обозначает деление! Это то же самое, что 1 разделить на 5 или Поэтому, когда 4 конфеты делить на двоих человек, получим дробь , а это 4 разделить на 2, каждый получит по 2 конфеты. Дробь
Верхнее число дроби, называется числителем, нижнее — знаменателем.
Зззззапомни зззззнаменатель внизззззу!!!!
Виды дробей
Дроби бывают положительными и отрицательными. Это зависит от того, какое число в числителе (сверху) — отрицательное или положительное. Знак «-» у отрицательной дроби принято писать перед чертой дроби. Можно его записать сверху, если так удобнее. Знак «+» обычно не пишут, аналогично положительным числам.
Дробь, у которой числитель меньше знаменателя, называется
Неправильную дробь можно записать смешанным числом (выделив целую часть)
Целая часть у дроби — это то же самое, что , однако знак «+» принято не записывать.
Особый вид чисел, которые можно представить в виде дробей — десятичные. У таких дробей в знаменателе 10 или 100, или 1000 и т.д.
Любое рациональное число можно обратить в конечную или бесконечную периодическую десятичную дробь. Например, является конечной дробью. Бесконечная десятичная дробь называется периодической, если у нее, начиная с некоторого места, одна цифра или группа цифр повторяется. Повторяющуюся группу цифр называют периодом и записывают в скобках. Например, или
Бесконечная десятичная непериодическая дробь представляется таким числом
Представление числа в виде дроби
Любое целое число представляется в виде дроби, знаменатель которой единица. При делении числа на единицу мы получаем то же число.
Если знаменатель и числитель дроби одинаковые числа, то эта дробь равна единице. При делении числа на себя получаем единицу.
Любая дробь, у которой числителем является ноль, равна нулю. Если ноль делить на любое число, получим ноль.
Не существует дроби, у которой в знаменателе ноль . Так как
Обратное число
Число называется обратным числу .
Например, числа взаимообратные.
Что такое дроби. Дроби обыкновенные правильные и неправильные, смешанные и составные
С дробями мы сталкиваемся в жизни гораздо раньше, чем начинается их изучение в школе. Если разрезать целое яблоко пополам, то мы получим часть фрукта — ½. Разрежем ещё раз — будет ¼. Это и есть дроби. И все, казалось бы, просто. Для взрослого человека. Для ребенка же (а данную тему начинают изучать в конце младшей школы) абстрактные математические понятия ещё пугающе непонятны, и преподаватель должен доступно объяснить, что такое правильная дробь и неправильная, обыкновенная и десятичная, какие операции можно с ними совершать и, главное, для чего всё это нужно.
Какие бывают дроби
Знакомство с новой темой в школе начинается с обыкновенных дробей. Их легко узнать по горизонтальной черте, разделяющей два числа — сверху и снизу. Верхнее называется числителем, нижнее — знаменателем. Существует и строчный вариант написания неправильных и правильных обыкновенных дробей — через косую черту, например: ½, 4/9, 384/183. Такой вариант используется, когда высота строки ограничена и нет возможности применить «двухэтажную» форму записи. Почему? Да потому что она удобнее. Чуть позже мы в этом убедимся.
Верхнее называется числителем, нижнее — знаменателем. Существует и строчный вариант написания неправильных и правильных обыкновенных дробей — через косую черту, например: ½, 4/9, 384/183. Такой вариант используется, когда высота строки ограничена и нет возможности применить «двухэтажную» форму записи. Почему? Да потому что она удобнее. Чуть позже мы в этом убедимся.
Помимо обыкновенных, существуют также десятичные дроби. Различить их очень просто: если в одном случае используется горизонтальная или наклонная черта, то в другом — запятая, разделяющая последовательности цифр. Посмотрим пример: 2,9; 163,34; 1,953. Мы намеренно воспользовались точкой с запятой в качестве разделителя, чтобы разграничить числа. Первое из них будет читаться так: «две целых, девять десятых».
Новые понятия
Вернемся к обыкновенным дробям. Они бывают двух видов.
Определение правильной дроби звучит следующим образом: это такая дробь, числитель которой меньше знаменателя. Почему это важно? Сейчас увидим!
У вас есть несколько яблок, разделенных на половинки. Всего — 5 частей. Как вы скажете: у вас «два с половиной» или «пять вторых» яблока? Конечно, первый вариант звучит естественнее, и при разговоре с друзьями мы воспользуемся им. А вот если потребуется посчитать, сколько фруктов достанется каждому, если в компании пять человек, мы запишем число 5/2 и разделим его на 5 — с точки зрения математики это будет нагляднее.
Всего — 5 частей. Как вы скажете: у вас «два с половиной» или «пять вторых» яблока? Конечно, первый вариант звучит естественнее, и при разговоре с друзьями мы воспользуемся им. А вот если потребуется посчитать, сколько фруктов достанется каждому, если в компании пять человек, мы запишем число 5/2 и разделим его на 5 — с точки зрения математики это будет нагляднее.
Итак, для наименования правильных и неправильных дробей правило таково: если в дроби можно выделить целую часть (14/5, 2/1, 173/16, 3/3), то она является неправильной. Если этого сделать нельзя, как в случае с ½, 13/16, 9/10, она будет правильной.
Основное свойство дроби
Если числитель и знаменатель дроби одновременно умножить или разделить на одно и то же число, её величина не изменится. Представьте: торт порезали на 4 равные части и дали вам одну. Такой же торт порезали на восемь частей и дали вам две. Не всё ли равно? Ведь ¼ и 2/8 — это одно и то же!
Сокращение
Авторы задач и примеров в учебниках по математике зачастую стремятся запутать учеников, предлагая громоздкие в написании дроби, которые на самом деле можно сократить. Вот пример правильной дроби: 167/334, который, казалось бы, выглядит очень «страшно». Но на самом деле мы можем записать его как ½. Число 334 делится на 167 без остатка — проделав такую операцию, мы получим 2.
Вот пример правильной дроби: 167/334, который, казалось бы, выглядит очень «страшно». Но на самом деле мы можем записать его как ½. Число 334 делится на 167 без остатка — проделав такую операцию, мы получим 2.
Смешанные числа
Неправильную дробь можно представить в форме смешанного числа. Это когда целая часть вынесена вперед и записана на уровне горизонтальной черты. Фактически выражение принимает вид суммы: 11/2 = 5 + ½; 13/6 = 2 + 1/6 и так далее.
Чтобы вынести целую часть, нужно разделить числитель на знаменатель. Остаток от деления записать сверху, над чертой, а целую часть — перед выражением. Таким образом, мы получаем две структурные части: целые единицы + правильную дробь.
Можно осуществить и обратную операцию — для этого нужно целую часть умножить на знаменатель и прибавить полученное значение к числителю. Ничего сложного.
Умножение и деление
Как ни странно, умножать дроби проще, чем складывать. Всего-то и требуется — продлить горизонтальную черту: (2/3) * (3/5) = 2*3 / 3*5 = 2/5.
С делением тоже всё просто: нужно перемножить дроби крест-накрест: (7/8) / (14/15) = 7*15 / 8*14 = 15/16.
Сложение дробей
Что делать, если требуется осуществить сложение или а в знаменателе у них разные числа? Поступить так же, как с умножением, не получится — здесь следует понимать определение правильной дроби и её сущность. Нужно привести слагаемые к общему знаменателю, то есть в нижней части обеих дробей должны оказаться одинаковые числа.
Чтобы это осуществить, следует воспользоваться основным свойством дроби: умножить обе части на одно и то же число. Например, 2/5 + 1/10 = (2*2)/(5*2) + 1/10 = 5/10 = ½.
Как же выбрать, к какому знаменателю приводить слагаемые? Это должно быть минимальное число, кратное обоим числам, стоящим в знаменателях дробей: для 1/3 и 1/9 это будет 9; для ½ и 1/7 — 14, потому что меньшего значения, делящегося без остатка на 2 и 7, не существует.
Использование
Для чего нужны неправильные дроби? Ведь гораздо удобнее сразу выделить целую часть, получить смешанное число — и дело с концом! Оказывается, если требуется выполнить умножение или деление двух дробей, выгоднее воспользоваться именно неправильными.
Возьмем следующий пример: (2 + 3/17) / (37 / 68).
Казалось бы, сократить и вовсе нечего. Но что, если записать результат сложения в первых скобках в виде неправильной дроби? Посмотрите: (37/17) / (37/68)
Теперь всё встает на свои места! Запишем пример таким образом, чтобы всё стало очевидно: (37*68) / (17*37).
Сократим 37 в числителе и знаменателе и, наконец, разделим верхнюю и нижнюю части на 17. Вы же помните основное правило для правильной и неправильной дроби? Мы можем умножать и делить их на любое число, если делаем это одновременно для числителя и знаменателя.
Итак, получаем ответ: 4. Пример выглядел сложным, а ответ содержит всего одну цифру. В математике так часто происходит. Главное — не бояться и следовать простым правилам.
Распространенные ошибки
При осуществлении учащийся может легко совершить одну из популярных ошибок. Обычно они происходят из-за невнимательности, а иногда — из-за того, что изученный материал ещё не отложился в голове как следует.
Нередко сумма чисел, стоящая в числителе, вызывает желание сократить отдельные её компоненты. Допустим, в примере: (13 + 2) / 13, написанном без скобок (с горизонтальной чертой), многие ученики по неопытности зачеркивают 13 сверху и снизу. Но так делать нельзя ни в коем случае, ведь это грубая ошибка! Если бы вместо сложения стоял знак умножения, мы получили бы в ответе число 2. Но при осуществлении сложения никакие операции с одним из слагаемых не позволительны, только со всей суммой целиком.
Ещё ребята часто ошибаются при делении дробей. Возьмем две правильные несократимые дроби и разделим друг на друга: (5/6) / (25/33). Ученик может перепутать и записать результирующее выражение как (5*25) / (6*33). Но так бы получилось при умножении, а в нашем случае всё будет несколько иначе: (5*33) / (6*25). Сокращаем то, что возможно, и в ответе увидим 11/10. Получившуюся неправильную дробь запишем как десятичную — 1,1.
Скобки
Помните, что в любых математических выражениях порядок действий определяется приоритетом знаков операций и наличием скобок. При прочих равных отсчёт очередности выполнения действий происходит слева направо. Это актуально и для дробей — выражение в числителе или знаменателе рассчитывается строго по этому правилу.
При прочих равных отсчёт очередности выполнения действий происходит слева направо. Это актуально и для дробей — выражение в числителе или знаменателе рассчитывается строго по этому правилу.
Ведь Это результат деления одного числа на другое. Если они не делятся нацело, получается дробь — вот и всё.
Как записать дробь на компьютере
Поскольку стандартные средства не всегда позволяют создать дробь, состоящую из двух «ярусов», ученики порой идут на различные ухищрения. Например, копируют числители и знаменатели в графический редактор «Пейнт» и склеивают их воедино, рисуя между ними горизонтальную линию. Конечно, есть более простой вариант, который, кстати, предоставляет и массу дополнительных возможностей, которые станут полезны вам в будущем.
Откройте «Майкрософт Ворд». Одна из панелей в верхней части экрана носит называние «Вставка» — нажмите её. Справа, в той стороне, где расположены значки закрытия и сворачивания окна, есть кнопка «Формула». Это именно то, что нам нужно!
Если вы воспользуетесь данной функцией, на экране появится прямоугольная область, в которой можно использовать любые математические знаки, отсутствующие на клавиатуре, а также писать дроби в классическом виде. То есть разделяя числитель и знаменатель горизонтальной чертой. Вы даже можете удивиться, что такую правильную дробь настолько легко записать.
То есть разделяя числитель и знаменатель горизонтальной чертой. Вы даже можете удивиться, что такую правильную дробь настолько легко записать.
Изучайте математику
Если вы учитесь в 5-6 классе, то уже скоро знание математики (в том числе — умение работать с дробями!) потребуется во многих школьных предметах. Практически в любой задаче по физике, при измерении массы веществ в химии, в геометрии и тригонометрии без дробей никак не обойтись. Уже скоро вы научитесь вычислять всё в уме, даже не записывая выражения на бумаге, но будут появляться всё более и более сложные примеры. Поэтому выучите, что такое правильная дробь и как с ней работать, не отставайте по учебной программе, своевременно делайте домашние задания, и тогда вы преуспеете.
1 Что такое обыкновенные дроби. Виды дробей.Дробь всегда означает какую то часть целого. Дело в том, что не всегда количество можно передать натуральными числами, то есть пересчитать: 1,2,3 и т.д. Как, например, обозначить половину арбуза или четверть часа? Вот для этого и появились дробные числа, или дроби.

Для начала нужно сказать, что вообще дробей бывает два вида: обыкновенные дроби и десятичные дроби. Обыкновенные дроби записываются так:
Десятичные дроби записываются по другому:
Обыкновенные дроби состоят из двух частей: вверху — числитель, внизу — знаменатель. Числитель и знаменатель разделяет дробная черта. Итак, запомните:
Любая дробь — это часть целого . За целое обычно принимают 1 (единицу). Знаменатель дроби показывает, на сколько частей разделили целое (1 ), а числитель — сколько частей взяли. Если мы разрезали торт на 6 одинаковых частей (в математике говорят долей ), то каждая часть торта будет равна 1/6. Если Вася съел 4 куска, то значит, он съел 4/6 .
С другой стороны, дробная черта — это не что иное, как знак деления. Поэтому дробь — это частное двух чисел — числителя и знаменателя. В тексте задач или в рецептах блюд дроби записываются обычно так: 2/3, 1/2 и т.д. Некоторые дроби получили собственное название, например, 1/2 — «половина», 1/3 — «треть», 1/4 — «четверть»
А теперь разберемся, какие бывают виды обыкновенных дробей.
2 Виды обыкновенных дробей
Обыкновенные дроби бывают трех видов: правильные, неправильные и смешанные:
Правильная дробь
Если числитель меньше, чем знаменатель, то такую дробь называют правильной, например: Правильная дробь всегда меньше 1.
Неправильная дробь
Если числитель больше, чем знаменатель или равен знаменателю, такая дробь называется неправильной , например:
Неправильная дробь больше единицы(если числитель больше знаменателя) или равна единице (если числитель равен знаменателю)
Смешанная дробь
Если дробь состоит из целого числа (целая часть) и правильной дроби (дробная часть), то такая дробь называется
Смешанная дробь всегда больше единицы.
3 Преобразования дробей
В математике обыкновенные дроби часто приходится преобразовывать, то есть смешанную дробь превращать в неправильную и наоборот. Это необходимо для выполнения некоторых действий, например, умножения и деления.
Это необходимо для выполнения некоторых действий, например, умножения и деления.
Итак, любую смешанную дробь можно перевести в неправильную . Для этого целую часть умножают на знаменатель и прибавляют числитель дробной части. Полученную сумму берут числителем, а знаменатель оставляют тот же, например:
Любую неправильную дробь можно превратить в смешанную. Для этого делят числитель на знаменатель (с остатком).Полученное число будет целой частью, а остаток — числителем дробной части, например:
При этом говорят: «Мы выделили целую часть из неправильной дроби».
Необходимо запомнить еще одно правило: Любое целое число можно представить в виде обыкновенной дроби со знаменателем 1 , например:
Поговорим о том, как сравнивать дроби.
4 Сравнение дробей
При сравнении дробей может быть несколько вариантов: Легко сравнивать дроби с одинаковыми знаменателями, гораздо сложнее — если знаменатели разные. А есть еще и сравнение смешанных дробей. Но не волнуйтесь, сейчас мы подробно рассмотрим каждый вариант и научимся сравнивать дроби.
А есть еще и сравнение смешанных дробей. Но не волнуйтесь, сейчас мы подробно рассмотрим каждый вариант и научимся сравнивать дроби.
Из двух дробей с одинаковыми знаменателями, но разными числителями больше та дробь, у которой числитель больше, например:
Из двух дробей с одинаковыми числителями, но разными знаменателями больше та дробь, у которой знаменатель меньше, например:
Неправильная или смешанная дробь всегда больше правильной дроби, например:
При сравнении двух смешанных дробей больше та дробь, у которой целая часть больше, например:
Если целые части у смешанных дробей одинаковые, больше та дробь, у которой дробная часть больше, например:
Сравнивать дроби с разными числителями и знаменателями без их преобразования нельзя. Сначала дроби нужно привести к одному знаменателю, а затем сравнить их числители. Больше та дробь, у которой числитель будет больше. А вот как приводить дроби к одинаковому знаменателю, мы рассмотрим в следующих двух разделах статьи статьи. Сначала мы рассмотрим основное свойство дроби и сокращение дробей, а затем непосредственно приведение дробей к одному знаменателю.
Сначала мы рассмотрим основное свойство дроби и сокращение дробей, а затем непосредственно приведение дробей к одному знаменателю.
5 Основное свойство дроби. Сокращение дробей. Понятие о НОД.
Запомните: складывать и вычитать, а также сравнивать можно только дроби, у которых одинаковые знаменатели . Если знаменатели разные, то сначала нужно привести дроби к одному знаменателю, то есть так преобразовать одну из дробей, чтобы ее знаменатель стал таким же, как у второй дроби.
У дробей есть одно важное свойство, называемое также основным свойством дроби:
Если и числитель, и знаменатель дроби умножить или разделить на одно и то же число, то величина дроби при этом не изменится :
Благодаря этому свойству мы можем сокращать дроби :
Сократить дробь — значит разделить и числитель, и знаменатель на одно и то же число (смотрите пример чуть выше). Когда мы сокращаем дробь, то можно расписать наши действия так:
Чаще же в тетради сокращают дробь так:
Но запомните: сокращать можно только множители. Если в числителе или знаменателе сумма или разность, сокращать слагаемые нельзя.
Пример:
Если в числителе или знаменателе сумма или разность, сокращать слагаемые нельзя.
Пример:
Нужно сначала преобразовать сумму в множитель:
Иногда, при работе с большими числами, для того, чтобы сократить дробь, удобно найти наибольший общий делитель числителя и знаменателя (НОД)
Наибольший общий делитель (НОД) нескольких чисел — это наибольшее натуральное число, на которое эти числа делятся без остатка.
Для того, чтобы найти НОД двух чисел (например, числителя и знаменателя дроби), нужно разложить оба числа на простые множители, отметить одинаковые множители в обоих разложениях, и перемножить эти множители. Полученное произведение и будет НОД. Например, нам нужно сократить дробь:
Найдем НОД чисел 96 и 36:
НОД нам показывает, что и в числителе, и в знаменателе есть множитель12, и мы легко сокращаем дробь.
Иногда, чтобы привести дроби к одному знаменателю, достаточно сократить одну из дробей. Но чаще бывает необходимо подбирать дополнительные множители для обеих дробей. Сейчас мы рассмотрим, как это делается. Итак:
Сейчас мы рассмотрим, как это делается. Итак:
6 Как приводить дроби к одному знаменателю. Наименьшее общее кратное (НОК).
Когда мы приводим дроби к одинаковому знаменателю, мы подбираем для знаменателя такое число, которое бы делилось и на первый, и на второй знаменатель (то есть было бы кратным обоим знаменателям, выражаясь математическим языком). И желательно, чтобы число это было как можно меньшим, так удобнее считать. Таким образом, мы должны найти НОК обоих знаменателей.
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.

- Перемножить все числа в произведении, это и будет НОК.
Например, найдем НОК чисел 28 и 21:
Однако вернемся к нашим дробям. После того, как мы подобрали или письменно вычислили НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом мы привели наши дроби к одному знаменателю — 15.
7 Сложение и вычитание дробей
Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Сложение и вычитание смешанных дробей с одинаковыми знаменателями
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью:
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
Вычитание проводится аналогично: целая часть вычитается из целой, а дробная — из дробной части:
Если дробная часть вычитаемого больше, чем дробная часть уменьшаемого, «занимаем» единицу из целой части, превращая уменьшаемое в неправильную дробь, а дальше действуем как обычно:
Аналогично вычитаем из целого числа дробь :
Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:
Если мы складываем целое число и смешанную дробь , мы прибавляем это число к целой части дроби, например:
Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как при сложении дробей с одинаковыми знаменателями (сложить числители):
При вычитании действуем аналогично:
Если работаем со смешанными дробями, приводим к одинаковому знаменателю их дробные части и далее вычитаем как обычно: целую часть из целой, а дробную — из дробной части:
8 Умножение и деление дробей.
Умножать и делить обыкновенные дроби гораздо проще, чем складывать и вычитать, так как не нужно приводить их к одному знаменателю. Запомните простые правила умножения и деления дробей:
Перед тем, как перемножать числа в числителе и знаменателе желательно сократить дробь, то есть избавиться от одинаковых множителей в числителе и знаменателе, как в нашем примере.
Чтобы разделить дробь на натуральное число , нужно знаменатель умножить на это число, а числитель оставить без изменений:
Например:
Деление дроби на дробь
Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное делителю (обратную дробь).Что же это за обратная дробь?
Если мы перевернем дробь, то есть поменяем местами числитель и знаменатель, то получим обратную дробь. Произведение дроби и обратной ей дроби дает единицу. В математике такие числа называют взаимно обратными числами:
Например, числа — взаимно обратные, так как
Таким образом, вернемся к делению дроби на дробь:
Чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю :
Например:
При делении смешанных дробей нужно так же, как и при умножении, сначала перевести их в неправильные дроби:
При умножении и делении дробей на целые натуральные числа , можно представлять эти числа так же в виде дробей со знаменателем 1 .
И при делении целого числа на дробь представляем это число в виде дроби со знаменателем 1 :
Примеры с дробями – один из основных элементов математики. Существует много разных типов уравнений с дробями. Ниже приведена подробная инструкция по решению примеров такого типа.
Как решать примеры с дробями – общие правила
Для решения примеров с дробями любых типов, будь то сложение, вычитание, умножение или деление, необходимо знать основные правила:
- Для того чтобы сложить дробные выражения с одинаковым знаменателем (знаменатель – число, находящееся в нижней части дроби, числитель – в верхней), нужно сложить их числители, а знаменатель оставить тем же.
- Для того чтобы вычесть от одного дробного выражения второе (с одинаковым знаменателем), нужно вычесть их числители, а знаменатель оставить тем же.
- Для того чтобы сложить или вычесть дробные выражения с разными знаменателями, нужно найти наименьший общий знаменатель.

- Для того чтобы найти дробное произведение, нужно перемножить числители и знаменатели, при этом, если есть возможность, сократить.
- Для того чтобы разделить дробь на дробь, нужно умножить первую дробь на перевернутую вторую.
Как решать примеры с дробями – практика
Правило 1, пример 1:
Вычислить 3/4 +1/4.
Согласно правилу 1, если у дробей двух (или больше) одинаковый знаменатель, нужно просто сложить их числители. Получим: 3/4 + 1/4 = 4/4. Если у дроби числитель и знаменатель одинаковы, такая дробь будет равна 1.
Ответ: 3/4 + 1/4 = 4/4 = 1.
Правило 2, пример 1:
Вычислить: 3/4 – 1/4
Пользуясь правилом номер 2, для решения этого уравнения нужно от 3 отнять 1, а знаменатель оставить тем же. Получаем 2/4. Так как два 2 и 4 можно сократить, сокращаем и получаем 1/2.
Ответ: 3/4 – 1/4 = 2/4 = 1/2.
Правило 3, Пример 1
Вычислить: 3/4 + 1/6
Решение: Пользуясь 3-м правилом, находим наименьший общий знаменатель. Наименьшим общим знаменателем называется такое число, которое делится на знаменатели всех дробных выражений примера. Таким образом, нам нужно найти такое минимальное число, которое будет делиться и на 4, и на 6. Таким числом является 12. Записываем в качестве знаменателя 12. 12 делим на знаменатель первой дроби, получаем 3, умножаем на 3, записываем в числителе 3*3 и знак +. 12 делим на знаменатель второй дроби, получаем 2, 2 умножаем на 1, записываем в числителе 2*1. Итак, получилась новая дробь со знаменателем, равным 12 и числителем, равным 3*3+2*1=11. 11/12.
Наименьшим общим знаменателем называется такое число, которое делится на знаменатели всех дробных выражений примера. Таким образом, нам нужно найти такое минимальное число, которое будет делиться и на 4, и на 6. Таким числом является 12. Записываем в качестве знаменателя 12. 12 делим на знаменатель первой дроби, получаем 3, умножаем на 3, записываем в числителе 3*3 и знак +. 12 делим на знаменатель второй дроби, получаем 2, 2 умножаем на 1, записываем в числителе 2*1. Итак, получилась новая дробь со знаменателем, равным 12 и числителем, равным 3*3+2*1=11. 11/12.
Ответ: 11/12
Правило 3, Пример 2:
Вычислить 3/4 – 1/6. Этот пример очень схож с предыдущим. Проделываем все те же действия, но в числителе вместо знака +, пишем знак минус. Получаем: 3*3-2*1/12 = 9-2/12 = 7/12.
Ответ: 7/12
Правило 4, Пример 1:
Вычислить: 3/4 * 1/4
Пользуясь четвертым правилом, умножаем знаменатель первой дроби на знаменатель второй и числитель первой дроби на числитель второй. 3*1/4*4 = 3/16.
3*1/4*4 = 3/16.
Ответ: 3/16
Правило 4, Пример 2:
Вычислить 2/5 * 10/4.
Данную дробь можно сократить. В случае произведения сокращаются числитель первой дроби и знаменатель второй и числитель второй дроби и знаменатель первой.
2 сокращается с 4. 10 сокращается с 5. получаем 1 * 2/2 = 1*1 = 1.
Ответ: 2/5 * 10/4 = 1
Правило 5, Пример 1:
Вычислить: 3/4: 5/6
Пользуясь 5-м правилом, получим: 3/4: 5/6 = 3/4 * 6/5. Сокращаем дробь по принципу предыдущего примера и получаем 9/10.
Ответ: 9/10.
Как решать примеры с дробями – дробные уравнения
Дробными уравнениями называются примеры, где в знаменателе есть неизвестное. Для того чтобы решить такое уравнение нужно пользоваться определенными правилами.
Рассмотрим пример:
Решить уравнение 15/3x+5 = 3
Вспомним, нельзя делить на ноль, т.е. значение знаменателя не должно равняться нулю. При решении таких примеров, это нужно обязательно указывать. Для этого существует ОДЗ (область допустимых значений).
Для этого существует ОДЗ (область допустимых значений).
Таким образом, 3x+5 ≠ 0.
Отсюда: 3x ≠ 5.
x ≠ 5/3
При x = 5/3 уравнение просто не имеет решения.
Указав ОДЗ, наилучшим способом решить данное уравнение будет избавиться от дробей. Для это сначала представим все не дробные значения в виде дроби, в данном случае число 3. Получим: 15/(3x+5) = 3/1. Чтобы избавиться от дроби нужно умножить каждую из них на наименьший общий знаменатель. В данном случае таковым будет (3x+5)*1. Последовательность действий:
- Умножаем 15/(3x+5) на (3x+5)*1 = 15*(3x+5).
- Раскрываем скобки: 15*(3x+5) = 45x + 75.
- То же самое проделываем с правой частью уравнения: 3*(3x+5) = 9x + 15.
- Приравниваем левую и правую часть: 45x + 75 = 9x +15
- Переносим иксы влево, числа вправо: 36x = – 50
- Находим x: x = -50/36.
- Сокращаем: -50/36 = -25/18
Ответ: ОДЗ x ≠ 5/3 . x = -25/18.
Как решать примеры с дробями – дробные неравенства
Дробные неравенства по типу (3x-5)/(2-x)≥0 решаются при помощи числовой оси. Рассмотрим данный пример.
Рассмотрим данный пример.
Последовательность действий:
- Приравниваем числитель и знаменатель к нулю: 1. 3x-5=0 => 3x=5 => x=5/3
2. 2-x=0 => x=2 - Чертим числовую ось, расписывая на ней получившиеся значения.
- Под значение рисуем кружок. Кружок бывает двух типов – заполненный и пустой. Заполненный кружок означает, что данное значение входит в ареал решений. Пустой круг говорит о том, что данное значение не входит в ареал решений.
- Так как знаменатель не может быть равным нулю, под 2-ой будет пустой круг.
- Чтобы определить знаки, подставляем в уравнение любое число больше двух, например 3. (3*3-5)/(2-3)= -4. значение отрицательное, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус.

- Так как нас интересуют значения икса, при котором выражение будет больше или равно 0, а таких значений нет (везде минусы), это неравенство не имеет решения, то есть x = Ø (пустое множество).
Ответ: x = Ø
Изучая царицу всех наук — математику, в определенный момент все сталкиваются с дробями. Хотя это понятие (как и сами виды дробей или математические действия с ними) совсем несложное, к нему нужно относиться внимательно, ведь в реальной жизни за пределами школы оно очень пригодится. Итак, давайте освежим свои знания о дробях: что это, для чего нужно, какие виды их бывают и как совершать с ними различные арифметические действия.
Ее величество дробь: это что такое
Дробями в математике называются числа, каждое из которых состоит из одной или более частей единицы. Такие дроби еще называют обыкновенными, либо простыми. Как правило, они записываются в виде двух чисел, которые разделены горизонтальной или слеш-чертой, она называется «дробной». Например: ½, ¾.
Например: ½, ¾.
Верхнее, или первое из этих чисел — это числитель (показывает, сколько взято долей от числа), а нижнее, или второе — знаменатель (демонстрирует, на столько частей разделена единица).
Дробная черта фактически выполняет функции знака деления. К примеру, 7:9=7/9
Традиционно обыкновенные дроби меньше единицы. В то время как десятичные могут быть больше ее.
Для чего нужны дроби? Да для всего, ведь в реальном мире далеко не все числа целые. К примеру, две школьницы в столовой купили в складчину одну вкусную шоколадку. Когда они уже собрались делить десерт, встретили подружку и решили угостить и и ее. Однако теперь необходимо правильно разделить шоколадку, если учесть, что она состоит из 12 квадратиков.
Поначалу девчонки хотели разделить все поровну, и тогда каждой бы досталось по четыре кусочка. Но, раздумав, они решили угостить подружку, не 1/3, а 1/4 шоколадки. А поскольку школьницы плохо изучали дроби, то они не учли, что при подобном раскладе в результате у них останется 9 кусочков, которые очень плохо делятся на двоих. Этот довольно простой пример показывает, насколько важно уметь правильно находить часть от числа. А ведь в жизни подобных случаев гораздо больше.
Этот довольно простой пример показывает, насколько важно уметь правильно находить часть от числа. А ведь в жизни подобных случаев гораздо больше.
Виды дробей: обыкновенные и десятичные
Все математические дроби делятся на два больших разряда: обыкновенные и десятичные. Об особенностях первого из них было рассказано в предыдущем пункте, так что теперь стоит уделить внимание второму.
Десятичной называют позиционную запись дроби числа, которая фиксируется на письме через запятую, без черточки или слеша. Например: 0,75, 0,5.
Фактически десятичная дробь идентична обыкновенной, однако, в ее знаменателе всегда единица с последующими нулями — отсюда произошло и ее название.
Число, предшествующее запятой, — это целая часть, а все находящееся после — дробная. Любую простую дробь можно перевести в десятичную. Так, указанные в предыдущем примере десятичные дроби можно записать как обычные: ¾ и ½.
Стоит отметить, что и десятичные, и обыкновенные дроби могут быть как положительными, так и отрицательными. Если перед ними стоит знак «-«, данная дробь отрицательная, если «+» — то положительная.
Если перед ними стоит знак «-«, данная дробь отрицательная, если «+» — то положительная.
Подвиды обыкновенных дробей
Есть такие виды дробей простых.
Подвиды десятичной дроби
В отличие от простой, десятичная дробь делится всего на 2 вида.
- Конечная — получила такое название из-за того, что после запятой у нее ограниченное (конечное) число цифр: 19,25.
- Бесконечная дробь — это число с нескончаемым количеством цифр после запятой. К примеру, при делении 10 на 3 результатом будет бесконечная дробь 3,333…
Сложение дробей
Проводить различные арифметические манипуляции с дробями немного сложнее, чем с обычными числами. Однако, если усвоить основные правила, решить любой пример с ними не составит особого труда.
Например: 2/3+3/4. Наименьшим общим кратным для них будет 12, следовательно, необходимо, чтобы в каждом знаменателе стояло это число. Для этого числитель и знаменатель первой дроби умножаем на 4, получается 8/12, аналогично поступаем со вторым слагаемым, но только множим на 3 — 9/12. Теперь можно легко решить пример: 8/12+9/12= 17/12. Получившаяся дробь — это неправильная величина, поскольку числитель больше знаменателя. Ее можно и нужно пребразовать в правильную смешанную, разделив 17:12= 1 и 5/12.
Теперь можно легко решить пример: 8/12+9/12= 17/12. Получившаяся дробь — это неправильная величина, поскольку числитель больше знаменателя. Ее можно и нужно пребразовать в правильную смешанную, разделив 17:12= 1 и 5/12.
В случае, если слагаются смешанные дроби, сначала действия совершаются с целыми числами, а потом с дробными.
Если в примере присутствует десятичная дробь и обычная, необходимо, чтобы обе стали простыми, потом привести их к одному знаменателю и сложить. К примеру 3,1+1/2. Число 3,1 можно записать как смешанную дробь 3 и 1/10 или как неправильную — 31/10. Общим знаменателем для слагаемых будет 10, поэтому нужно умножить поочередно числитель и знаменатель 1/2 на 5, получается 5/10. Далее можно легко все высчитать: 31/10+5/10=35/10. Полученный результат — неправильная сократимая дробь, приводим ее в нормальный вид, сократив на 5: 7/2=3 и 1/2, или десятичной — 3,5.
Если слагать 2 десятичные дроби, важно, чтобы после запятой было одинаковое количество цифр. Если это не так, нужно просто дописать необходимое количество нулей, ведь в десятичной дроби это можно сделать безболезненно. Например, 3,5+3,005. Чтобы решить это задание, нужно к первому числу прибавить 2 ноля и далее поочередно слагать: 3,500+3,005=3,505.
Например, 3,5+3,005. Чтобы решить это задание, нужно к первому числу прибавить 2 ноля и далее поочередно слагать: 3,500+3,005=3,505.
Вычитание дробей
Вычитая дроби, стоит поступать так же, как и при сложении: свести к общему знаменателю, отнять один числитель от другого, при необходимости перевести результат в смешанную дробь.
Например: 16/20-5/10. Общим знаменателем будет 20. Нужно привести вторую дробь к этому знаменателю, умножив обе ее части на 2, получается 10/20. Теперь можно решать пример: 16/20-10/20= 6/20. Однако этот результат относится к сократимым дробям, поэтому стоит поделить обе части на 2 и получается результат — 3/10.
Умножение дробей
Деление и умножение дробей — значительно более простые действия, нежели сложение и вычитание. Дело в том, что, выполняя эти задания, нет необходимости искать общий знаменатель.
Чтобы умножить дроби, нужно просто поочередно перемножить между собою оба числителя, а затем и оба знаменателя. Получившийся результат сократить, если дробь — это сократимая величина.
Например: 4/9х5/8. После поочередного умножения получается такой результат 4х5/9х8=20/72. Такая дробь сократима на 4, поэтому конечный ответ в примере — 5/18.
Как делить дроби
Деление дробей — тоже несложное действие, фактически оно все равно сводится к их умножению. Чтобы разделить одну дробь на другую, нужно вторую перевернуть и умножить на первую.
Например, деление дробей 5/19 и 5/7. Чтобы решить пример, нужно поменять местами знаменатель и числитель второй дроби и умножить: 5/19х7/5=35/95. Результат можно сократить на 5 — получается 7/19.
В случае, если необходимо разделить дробь на простое число, методика немного отличается. Изначально стоит записать это число как неправильную дробь, а потом делить по той же схеме. Например, 2/13:5 нужно записать как 2/13: 5/1. Теперь нужно перевернуть 5/1 и умножить получившиеся дроби: 2/13х1/5= 2/65.
Иногда приходится совершать деление дробей смешанных. С ними нужно поступать, как и с целыми числами: превратить в неправильные дроби, перевернуть делитель и умножить все. Например, 8 ½: 3. Превращаем все в неправильные дроби: 17/2: 3/1. Далее следует переворот 3/1 и умножение: 17/2х1/3= 17/6. Теперь следует перевести неправильную дробь в правильную — 2 целых и 5/6.
Например, 8 ½: 3. Превращаем все в неправильные дроби: 17/2: 3/1. Далее следует переворот 3/1 и умножение: 17/2х1/3= 17/6. Теперь следует перевести неправильную дробь в правильную — 2 целых и 5/6.
Итак, разобравшись с тем, что такое дроби и как можно с ними совершать различные арифметические действия, нужно постараться не забывать об этом. Ведь люди всегда более склонны делить что-то на части, нежели прибавлять, поэтому нужно уметь делать это правильно.
Числитель и знаменатель дроби. Виды дробей. Продолжаем рассматривать дроби. Сначала небольшая оговорка – мы, рассматривая дроби и соответствующие примеры с ними, пока будем работать только с числовым её представлением. Бывают ещё и дробные буквенные выражения (с числами и без них). Впрочем, все «принципы» и правила также распространяются и на них, но о таких выражениях поговорим в будущем отдельно. Рекомендую посетить и изучать (вспоминать) тему дробей шаг за шагом.
Самое главное понять, запомнить и осознать, что ДРОБЬ – это ЧИСЛО!!!
Обыкновенная дробь – это число вида:
Число расположенное «сверху» (в данном случае m) называется числителем, число расположенное снизу (число n) называется знаменателем. У тех, кто только коснулся темы частенько возникает путаница – что как называется.
У тех, кто только коснулся темы частенько возникает путаница – что как называется.
Вот вам приёмчик, как навсегда запомнить – где числитель, а где знаменатель. Данный приём связан со словесно-образной ассоциацией. Представьте себе банку с мутной водой. Известно, что по мере отстоя воды чистая вода остаётся сверху, а муть (грязь) оседает, запоминаем:
ЧИССС тая вода ВВЕРХУ (ЧИССС литель сверху)
ГряЗЗЗННН ая вода ВНИЗУ (ЗННН аменатель внизу)
Так что, как только возникнет необходимость вспомнить, где числитель, а где знаменатель, то сразу зрительно представили банку с отстоянной водой, в которой сверху ЧИСтая вода, а снизу гряЗНая вода. Есть и другие приёмы для запоминания, если они вам помогут, то хорошо.
Примеры обыкновенных дробей:
Что означает горизонтальная черточка между числами? Это не что иное, как знак деления. Получается, что дробь можно рассматривать как бы как пример с действием делением. Просто записано это действие вот в таком виде. То есть, верхнее число (числитель) делится на нижнее (знаменатель):
Кроме того, есть ещё форма записи – дробь может записываться и так (через косую черту):
1/9, 5/8, 45/64, 25/9, 15/13, 45/64 и так далее…
Можем записать вышеуказанные нами дроби так:
Результат деления, как известно это число.
Уяснили – ДРОБЬ ЭТО ЧИСЛО!!!
Как вы уже заметили, у обыкновенной дроби числитель может быть меньше знаменателя, может быть больше знаменателя и может быть равен ему. Тут присутствует множество важных моментов, которые понятны интуитивно, без каких-либо теоретических изысков. Например:
1. Дроби 1 и 3 можно записать как 0,5 и 0,01. Забежим немного вперёд – это десятичные дроби, о них поговорим чуть ниже.
2. Дроби 4 и 6 в результате дают целое число 45:9=5, 11:1 = 11.
3. Дробь 5 в результате даёт единицу 155:155 = 1.
Какие выводы напрашиваются сами собой? Следующие:
1. Числитель при делении на знаменатель может дать конечное число. Может и не получится, разделите столбиком 7 на 13 или 17 на 11 — никак! Делить можно бесконечно, но об этом также поговорим чуть ниже.
2. Дробь в результате может дать целое число. Следовательно и любое целое число мы можем представить в виде дроби, вернее бесконечного ряда дробей, посмотрите, все эти дроби равны 2:
Ещё! Любое целое число мы всегда можем записать в виде дроби – само это число в числителе, единица в знаменателе:
3. Единицу мы всегда можем представить в виде дроби с любым знаменателем:
Единицу мы всегда можем представить в виде дроби с любым знаменателем:
*Указанные моменты крайне важны для работы с дробями при вычислениях и преобразованиях.
Виды дробей.
А теперь о теоретическом разделении обыкновенных дробей. Их разделяют на правильные и неправильные .
Дробь у которой числитель меньше знаменателя называется правильной. Примеры:
Дробь у которой числитель больше знаменателя или равен ему называется неправильной. Примеры:
Смешанная дробь (смешанное число).
Смешанной дробью называется дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дробной его части. Примеры:
Смешанную дробь всегда можно представить в виде неправильной дроби и наоборот. Идём далее!
Десятичные дроби.
Выше мы их уже затронули, это примеры (1) и (3), теперь подробнее. Вот примеры десятичных дробей: 0,3 0,89 0,001 5,345.
Дробь, знаменатель которой есть степень числа 10, например 10, 100, 1000 и так далее, называется десятичной. Записать первые три указанные дроби в виде обыкновенных дробей несложно:
Записать первые три указанные дроби в виде обыкновенных дробей несложно:
Четвёртая является смешанной дробью (смешанным числом):
Десятичная дробь имеет следующую форму записи — с начала целая часть, затем разделитель целой и дробной части точка или запятая и затем дробная часть, количество цифр дробной части строго определяется размерностью дробной части: если это десятые доли, дробная часть записывается одной цифрой; если тысячные — тремя; десятитысячные — четырьмя и т. д.
Данные дроби бывают конечными и бесконечными.
Примеры конечных десятичных дробей: 0,234; 0,87; 34,00005; 5,765.
Примеры бесконечных. Например число Пи это бесконечная десятичная дробь, ещё – 0,333333333333…… 0,16666666666…. и прочие. Также результат извлечения корня из чисел 3, 5, 7 и т.д. будет являться бесконечной дробью.
Дробная часть может быть цикличная (в ней присутствует цикл), два примера выше именно такие, ещё примеры:
0,123123123123…… цикл 123
0,781781781718…. .. цикл 781
.. цикл 781
0,0250102501…. цикл 02501
Записать их можно как 0,(123) 0,(781) 0,(02501).
Число Пи не является цикличной дробью как и, например, корень из трёх.
Ниже в примерах, будут звучать такие слова как «переворачиваем» дробь – это означает что числитель и знаменатель меняем местами. На самом деле у такой дроби есть название – обратная дробь. Примеры взаимно-обратных дробей:
Небольшой итог! Дроби бывают:
Обыкновенные (правильные и неправильные).
Десятичные (конечные и бесконечные).
Смешанные (смешанные числа).
На этом всё!
С уважением, Александр.
Обыкновенные дроби
Вопросы занятия:
· повторить понятие «обыкновенная дробь», виды обыкновенных дробей;
· повторить основное свойство дроби;
· вспомнить, как неправильную дробь можно представить в виде смешанной или целого числа, а также как смешанную дробь можно представить в виде неправильной;
· повторить порядок выполнения действий над обыкновенными
дробями.
Материал урока
Мы ранее рассматривали случаи, когда нельзя выполнить целочисленное деление. В таких ситуациях можно частное записать в виде дроби. Делимое тогда называют числителем, а делитель — знаменателем. Отделяет их друг от друга черта дроби.
Как вам известно выделяют правильные и неправильные обыкновенные дроби. Напомним их отличия.
Напомним основное свойство дроби.
Числитель и знаменатель дроби можно умножать и делить на одно и тоже число, при этом значение дроби останется тем же.
Определение.
Умножение числителя и знаменателя на некоторое число называют приведением к новому знаменателю. Это позволяет приводить дроби к общему знаменателю.
Обычно дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Определение.
Процесс
деления числителя и знаменателя на некоторое число мы привыкли называть сокращением.
Обычно сократимую дробь сокращают на наибольший общий делитель числителя и знаменателя. Тем самым в итоге получают несократимую дробь. И к такому виду принято приводить все дроби, полученные в результате вычислений, прежде чем записать ответ. Дробь является несократимой, если числитель и знаменатель являются взаимно простыми числами.
Пример.
А теперь сократим дроби.
Пример.
Вам хорошо известно, что у любой неправильной дроби можно выделить целую часть.
Напомним, как это можно сделать.
Можно разделить числитель на знаменатель с остатком.
Частное будет целой частью, остаток — числителем дробной части, а исходный знаменатель — знаменателем дробной части.
Так из неправильной дроби мы получим смешанную.
Пример.
Далее вспомним правила сравнения обыкновенных дробей.
Если
же у дробей разные числители и разные знаменатели, то пользуясь основным
свойством дроби их можно привести или к равным знаменателям, или к равным
числителям.
В работе с дробями нужно уметь не только выделять целую часть у неправильных дробей, а ещё и представлять смешанные дроби в виде неправильных. Напомним, как это можно сделать.
Для этого в числитель записывают произведение целой части и знаменателя, увеличенного на числитель исходной дроби. Ну, а знаменатель оставляют тем же.
Пример.
Далее подробнее поговорим о выполнении арифметических действий с дробями.
Складывая дроби с одинаковыми знаменателями, в числитель записываем сумму числителей, а знаменатель оставляем тем же.
Если же нужно сложить дроби с разными знаменателями, предварительно их нужно привести к общему и сложить полученные дроби.
Пример.
Вычитание
дробей с одинаковыми знаменателями проводят по аналогичному правилу. В
числитель записывают разность числителей, а знаменатель оставляют тем же.
Для вычитания дробей с разными знаменателями, их сначала нужно привести к общему знаменателю, а затем вычислить разность полученных дробей.
Пример.
Теперь поговорим об умножении дробей.
Чтобы умножить дробь на число нужно только числитель умножить на это число, а знаменатель оставить тем же.
Произведением двух дробей является дробь, у которой числитель равен произведению числителей исходных дробей, а знаменатель — произведению знаменателей исходных дробей.
К тому же вам известно, что, если среди дробей множителей есть смешанные дроби, то их нужно предварительно представить в виде неправильных.
Пример.
А теперь самое время вспомнить понятие взаимно обратных чисел.
Определение.
Взаимно обратными называют 2 числа, произведение которых равно единице.
Например,
Вернёмся
к действиям с дробями и рассмотрим последнее — деление дробей.
Прежде чем приступить к делению, смешанные дроби так же нужно представлять в виде неправильных, и далее пользоваться таким правилом.
Знак деления нужно заменить умножением и дробь-делитель заменить обратной ей дробью. А далее следовать по правилу умножения дробей.
Пример.
Пример.
Итоги урока
Подводя итоги урока, вспомним, какие вопросы мы на нём осветили.
Мы вспомнили, что обыкновенные дроби бывают правильными и неправильными, а также повторили основное свойство дроби, которое позволяет сокращать дроби и приводить их к новому знаменателю.
Вспомнили, как неправильную дробь можно представить в виде смешанной или в виде целого числа, а также как смешанную дробь можно представить в виде неправильной.
И, освежив в памяти правила выполнения действий над
обыкновенными дробями, мы применили их при вычислении значений выражений.
Виды дробей и основное свойство дроби
Обыкновенная дробь — это частное двух натуральных чисел, одно из которых записано в числителе дроби, а второе — в знаменателе. Виды обыкновенных дробей определяются сравнением числителя и знаменателя дроби.
Определение. Если числитель дроби (натуральное число) меньше ее знаменателя (натурального числа), то дробь называется правильной.
Например:
Определение. Если числитель дроби (натуральное число) больше ее знаменателя (натурального числа) или равен ему, то дробь называется неправильной.
Например:
Перевод неправильной дроби в смешанную дробь — это выделение натурального числа из дроби.
Определение. Если дробь состоит из натурального числа (целая часть) и правильной дроби (дробная часть), то такая дробь называется смешанной (дробное число).
Например:
Правило. Любую смешанную дробь можно перевести в неправильную, для чего нужно целую часть умножить на знаменатель дробной части и к произведению прибавить числитель дробной части, сумму взять числителем, подписав тот же знаменатель.
Любую смешанную дробь можно перевести в неправильную, для чего нужно целую часть умножить на знаменатель дробной части и к произведению прибавить числитель дробной части, сумму взять числителем, подписав тот же знаменатель.
Например:
Правило. Любую неправильную дробь можно заменить смешанной дробью, для этого необходимо числитель неправильной дроби разделить на ее знаменатель, полученное частное взять целой частью дроби, а остаток (если он есть) — числителем дробной части смешанной дроби, подписав под ним тот же знаменатель.
Например:
Основное свойство дроби
Правило. Числитель и знаменатель дроби можно умножать (делить) на одно и то же натуральное число, от этого величина дроби не изменяется.
Основное свойство дроби используется при сокращении дробей и при приведении двух и более дробей к одинаковому знаменателю.
Правило. Любое натуральное число можно записать в виде обыкновенной дроби со знаменателем 1 (единица). Такая дробь будет неправильной.
Такая дробь будет неправильной.
Например:
Дробные числа, виды дробных чисел. «Альфа-школа».
Дробью называют отношение двух чисел \(\frac{m}{n}\), где m-делимое, а \(n\)- делитель, \(m\) – числитель, \(n\) – знаменатель.
Первое упоминание дробного числа было в Египте и Вавилоне. Происхождение дробного числа прочно и неделимо связано с решением практических задач в жизни людей. Понятие дроби содержит арабские корни и возникает от слова, именованного “ломать, разделять». В наше время значение слова не поменялось. Две страны по-разному объясняли дробь. Изначально была введена дробь \(\frac{1}{2}\). Дальше появились \(\frac{1}{3}\), \(\frac{1}{4}\) ,\(\frac{1}{5}\) и так далее. Первые упоминание, согласно данным археологов, появилось около \(5\) тысяч лет.
Египетские дроби мало чем отличаются от дробей, представленных сегодня. Египтяне при подсчетах все доли старались записывать в виде слагаемых: \(\frac{1}{2}\)+ \(\frac{1}{3}\) + \(\frac{1}{6}\), в отдельности записывались \(\frac{3}{4}\) и \(\frac{5}{7}\) и т. д., вводились таблицы для записи долей числа.
д., вводились таблицы для записи долей числа.
Довольно интересное представление сложилось в Вавилоне. Основываясь на шумерской шестнадцатеричной системе счисления, каждый новый разряд дроби у них был кратным \(60\). Это дало толчок для зарождения систем времени и меры углов в наше время.
Если число m можно разделить на одинаковое число, то дробь сократимая, если нельзя, то дробь несократимая. Из вышесказанного можно сформулировать основное свойство дроби:
если m и n умножить или поделить на одинаковое число, величина не видоизменится.
Дроби бывают:
- правильные — \(m\) меньше \(n\);
- неправильные — \(m\) больше или равен \(n\).
Смешанные дроби — это неправильные дроби, где можно выделить целую часть.
Обратные дроби — это когда мы меняем числитель и знаменатель у правильной дроби.Чтобы найти обратную дробь у смешанной, нам нужно сначала перевести ее в неправильную дробь, а затем перевернуть.
Составная дробь содержит отношение двух дробей, например: \( \frac{\frac{1}{2} }{\frac{1}{7}}\)
Задача 1. Найти обратную дробь у числа \(2\frac{1}{2}\).
Решение.
- в смешанной дроби \(2*2+1 =5\) числитель, \(2\) знаменатель
- \(\) \(\frac{5}{2}\) неправильная дробь, затем переворачиваем ее и получаем
Рассмотрим дробное число 4\(\frac{4}{3}\). Таким образом, \(4\) в знаменателе числа \(\frac{3}{4}\) означает, что мы разбиваем целое число на \(4\) равные части. И \(3\) в \(\frac{3}{4}\) говорит нам, что эта доля представляет собой сумму \(3\) долей. Достаточно просто. Теперь давайте взглянем на то, что это все означает, когда вы делаете простое сложение и привидение знаменателей.
Задача 2. Определите какие это дроби \(\frac{6}{8}\) ,\(\frac{7}{5}\), \(\frac{6}{6}\), \(\frac{7}{8}\), \(\frac{5}{6}\) ,\(\frac{9}{8}\)?
- \(\frac{6}{8}\),7\(\frac{7}{8}\),\(\frac{5}{6}\) – правильные дроби, так как \(8>6\), \(7>5\) , \(6>5\)
- \(\frac{6}{6}\) ,\(\frac{7}{5}\), \(\frac{9}{8}\) – неправильные дроби, также они являются смешанными так как \(6=6\), \(7>5\), \(9>8\) и можно выделить целую часть \(1\), \(1\frac{1}{2}\), \(1\frac{1}{18}\) соответсвенно.

Еще больше примеров и задач ты сможешь решить с онлайн школой myalfaschool.ru .
Десятичные дроби. Обо Всём Чем отличается обыкновенная дробь от десятичной
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Дроби в старших классах не сильно досаждают. До поры до времени. Пока не столкнётесь со степенями с рациональными показателями да логарифмами. А вот там…. Давишь, давишь калькулятор, а он все полное табло каких-то циферок кажет. Приходится головой думать, как в третьем классе.
Давайте уже разберёмся с дробями, наконец! Ну сколько можно в них путаться!? Тем более, это всё просто и логично. Итак, какие бывают дроби?
Виды дробей. Преобразования.
Дроби бывают трёх видов.
1. Обыкновенные дроби , например:
Иногда вместо горизонтальной чёрточки ставят наклонную черту: 1/2, 3/4, 19/5, ну, и так далее. Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем , нижнее — знаменателем. Если вы постоянно путаете эти названия (бывает…), скажите себе с выражением фразу: «Ззззз апомни! Ззззз наменатель — вниззззз у!» Глядишь, всё и ззззапомнится.)
Здесь мы часто будем таким написанием пользоваться. Верхнее число называется числителем , нижнее — знаменателем. Если вы постоянно путаете эти названия (бывает…), скажите себе с выражением фразу: «Ззззз апомни! Ззззз наменатель — вниззззз у!» Глядишь, всё и ззззапомнится.)
Чёрточка, что горизонтальная, что наклонная, означает деление верхнего числа (числителя) на нижнее (знаменатель). И всё! Вместо чёрточки вполне можно поставить знак деления — две точки.
Когда деление возможно нацело, это надо делать. Так, вместо дроби «32/8» гораздо приятнее написать число «4». Т.е. 32 просто поделить на 8.
32/8 = 32: 8 = 4
Я уж и не говорю про дробь «4/1». Которая тоже просто «4». А если уж не делится нацело, так и оставляем, в виде дроби. Иногда приходится обратную операцию проделывать. Делать из целого числа дробь. Но об этом далее.
2. Десятичные дроби , например:
Именно в таком виде нужно будет записывать ответы на задания «В».
3. Смешанные числа , например:
Смешанные числа практически не используются в старших классах. Для того, чтобы с ними работать, их всяко надо переводить в обыкновенные дроби. Но это точно надо уметь делать! А то попадётся такое число в задачке и зависните… На пустом месте. Но мы-то вспомним эту процедуру! Чуть ниже.
Наиболее универсальны обыкновенные дроби . С них и начнём. Кстати, если в дроби стоят всякие логарифмы, синусы и прочие буковки, это ничего не меняет. В том смысле что все действия с дробными выражениями ничем не отличаются от действий с обыкновенными дробями !
Основное свойство дроби.
Итак, поехали! Для начала я вас удивлю. Всё многообразие преобразований дробей обеспечивается одним-единственным свойством! Оно так и называется, основное свойство дроби . Запоминайте: если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится. Т.е:
Понятно, что писать можно дальше, до посинения. Синусы и логарифмы пусть вас не смущают, с ними дальше разберёмся. Главное понять, что все эти разнообразные выражения есть одна и та же дробь . 2/3.
Синусы и логарифмы пусть вас не смущают, с ними дальше разберёмся. Главное понять, что все эти разнообразные выражения есть одна и та же дробь . 2/3.
А оно нам надо, все эти превращения? Ещё как! Сейчас сами увидите. Для начала употребим основное свойство дроби для сокращения дробей . Казалось бы, вещь элементарная. Делим числитель и знаменатель на одно и то же число и все дела! Ошибиться невозможно! Но… человек — существо творческое. Ошибиться везде может! Особенно, если приходится сокращать не дробь типа 5/10, а дробное выражение со всякими буковками.
Как правильно и быстро сокращать дроби, не делая лишней работы, можно прочитать в особом Разделе 555 .
Нормальный ученик не заморачивается делением числителя и знаменателя на одно и то же число (или выражение)! Он просто зачеркивает всё одинаковое сверху и снизу! Здесь-то и таится типичная ошибка, ляп, если хотите.
Например, надо упростить выражение:
Тут и думать нечего, зачеркиваем букву «а» сверху и двойку снизу! Получаем:
Все правильно. Но реально вы поделили весь числитель и весь знаменатель на «а». Если вы привыкли просто зачеркивать, то, впопыхах, можете зачеркнуть «а» в выражении
Но реально вы поделили весь числитель и весь знаменатель на «а». Если вы привыкли просто зачеркивать, то, впопыхах, можете зачеркнуть «а» в выражении
и получить снова
Что будет категорически неверно. Потому что здесь весь числитель на «а» уже не делится ! Эту дробь сократить нельзя. Кстати, такое сокращение – это, гм… серьезный вызов преподавателю. Такого не прощают! Запомнили? При сокращении делить надо весь числитель и весь знаменатель!
Сокращение дробей сильно облегчает жизнь. Получится где-нибудь у вас дробь, к примеру 375/1000. И как теперь с ней дальше работать? Без калькулятора? Умножать, скажем, складывать, в квадрат возводить!? А если не полениться, да аккуратненько сократить на пять, да ещё на пять, да ещё… пока сокращается, короче. Получим 3/8! Куда приятнее, правда?
Основное свойство дроби позволяет переводить обыкновенные дроби в десятичные и наоборот без калькулятора ! Это важно на ЕГЭ, верно?
Как переводить дроби из одного вида в другой.

С десятичными дробями всё просто. Как слышится, так и пишется! Скажем, 0,25. Это ноль целых, двадцать пять сотых. Так и пишем: 25/100. Сокращаем (делим числитель и знаменатель на 25), получаем обычную дробь: 1/4. Всё. Бывает, и не сокращается ничего. Типа 0,3. Это три десятых, т.е. 3/10.
А если целых — не ноль? Ничего страшного. Записываем всю дробь без всяких запятых в числитель, а в знаменатель — то, что слышится. Например: 3,17. Это три целых, семнадцать сотых. Пишем в числитель 317, а в знаменатель 100. Получаем 317/100. Ничего не сокращается, значит всё. Это ответ. Элементарно, Ватсон! Из всего сказанного полезный вывод: любую десятичную дробь можно превратить в обыкновенную .
А вот обратное преобразование, обыкновенной в десятичную, некоторые без калькулятора не могут сделать. А надо! Как вы ответ записывать будете на ЕГЭ!? Внимательно читаем и осваиваем этот процесс.
Десятичная дробь чем характерна? У неё в знаменателе всегда стоит 10, или 100, или 1000, или 10000 и так далее. Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, 4/10 = 0,4. Или 7/100 = 0,07. Или 12/10 = 1,2. А если в ответе на задание раздела «В» получилось 1/2? Что в ответ писать будем? Там десятичные требуются…
Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, 4/10 = 0,4. Или 7/100 = 0,07. Или 12/10 = 1,2. А если в ответе на задание раздела «В» получилось 1/2? Что в ответ писать будем? Там десятичные требуются…
Вспоминаем основное свойство дроби ! Математика благосклонно позволяет умножать числитель и знаменатель на одно и то же число. На любое, между прочим! Кроме нуля, разумеется. Вот и применим это свойство себе на пользу! На что можно умножить знаменатель, т.е. 2 чтобы он стал 10, или 100, или 1000 (поменьше лучше, конечно…)? На 5, очевидно. Смело умножаем знаменатель (это нам надо) на 5. Но, тогда и числитель надо умножить тоже на 5. Это уже математика требует! Получим 1/2 = 1х5/2х5 = 5/10 = 0,5. Вот и всё.
Однако, знаменатели всякие попадаются. Попадётся, например дробь 3/16. Попробуй, сообрази тут, на что 16 умножить, чтоб 100 получилось, или 1000… Не получается? Тогда можно просто разделить 3 на 16. За отсутствием калькулятора делить придётся уголком, на бумажке, как в младших классах учили. Получим 0,1875.
Получим 0,1875.
А бывают и совсем скверные знаменатели. Например, дробь 1/3 ну никак не превратишь в хорошую десятичную. И на калькуляторе, и на бумажке, мы получим 0,3333333… Это значит, что 1/3 в точную десятичную дробь не переводится . Так же, как и 1/7, 5/6 и так далее. Много их, непереводимых. Отсюда ещё один полезный вывод. Не каждая обыкновенная дробь переводится в десятичную !
Кстати, это полезная информация для самопроверки. В разделе «В» в ответ надо десятичную дробь записывать. А у вас получилось, например, 4/3. Эта дробь не переводится в десятичную. Это означает, что где-то вы ошиблись по дороге! Вернитесь, проверьте решение.
Итак, с обыкновенными и десятичными дробями разобрались. Осталось разобраться со смешанными числами. Для работы с ними их всяко нужно перевести в обыкновенные дроби. Как это сделать? Можно поймать шестиклассника и спросить у него. Но не всегда шестиклассник окажется под руками… Придётся самим. Это несложно. Надо знаменатель дробной части умножить на целую часть и прибавить числитель дробной части. Это будет числитель обычной дроби. А знаменатель? Знаменатель останется тем же самым. Звучит сложно, но на деле всё элементарно. Смотрим пример.
Надо знаменатель дробной части умножить на целую часть и прибавить числитель дробной части. Это будет числитель обычной дроби. А знаменатель? Знаменатель останется тем же самым. Звучит сложно, но на деле всё элементарно. Смотрим пример.
Пусть в задачке вы с ужасом увидели число:
Спокойно, без паники соображаем. Целая часть — это 1. Единица. Дробная часть — 3/7. Стало быть, знаменатель дробной части — 7. Этот знаменатель и будет знаменателем обыкновенной дроби. Считаем числитель. 7 умножаем на 1 (целая часть) и прибавляем 3 (числитель дробной части). Получим 10. Это будет числитель обыкновенной дроби. Вот и всё. Еще проще это выглядит в математической записи:
Ясненько? Тогда закрепите успех! Переведите в обыкновенные дроби. У вас должно получится 10/7, 7/2, 23/10 и 21/4.
Обратная операция — перевод неправильной дроби в смешанное число — в старших классах редко требуется. Ну если уж… И если Вы — не в старших классах — можете заглянуть в особый Раздел 555 . Там же, кстати, и про неправильные дроби узнаете.
Там же, кстати, и про неправильные дроби узнаете.
Ну вот, практически и всё. Вы вспомнили виды дробей и поняли, как переводить их из одного вида в другой. Остаётся вопрос: зачем это делать? Где и когда применять эти глубокие познания?
Отвечаю. Любой пример сам подсказывает необходимые действия. Если в примере смешались в кучу обыкновенные дроби, десятичные, да ещё и смешанные числа, переводим всё в обыкновенные дроби. Это всегда можно сделать . Ну а если написано, что-нибудь типа 0,8 + 0,3, то так и считаем, безо всякого перевода. Зачем нам лишняя работа? Мы выбираем тот путь решения, который удобен нам !
Если в задании сплошь десятичные дроби, но гм… злые какие-то, перейдите к обыкновенным, попробуйте! Глядишь, всё и наладится. Например, придется в квадрат возводить число 0,125. Не так-то просто, если от калькулятора не отвыкли! Мало того, что числа перемножать столбиком надо, так ещё думай, куда запятую вставить! В уме точно не получится! А если перейти к обыкновенной дроби?
0,125 = 125/1000. Сокращаем на 5 (это для начала). Получаем 25/200. Ещё раз на 5. Получаем 5/40. О, ещё сокращается! Снова на 5! Получаем 1/8. Легко возводим в квадрат (в уме!) и получаем 1/64. Всё!
Сокращаем на 5 (это для начала). Получаем 25/200. Ещё раз на 5. Получаем 5/40. О, ещё сокращается! Снова на 5! Получаем 1/8. Легко возводим в квадрат (в уме!) и получаем 1/64. Всё!
Подведём итоги этого урока.
1. Дроби бывают трёх видов. Обыкновенные, десятичные и смешанные числа.
2. Десятичные дроби и смешанные числа всегда можно перевести в обыкновенные дроби. Обратный перевод не всегда возможен.
3. Выбор вида дробей для работы с заданием зависит от этого самого задания. При наличии разных видов дробей в одном задании, самое надёжное — перейти к обыкновенным дробям.
Теперь можно потренироваться. Для начала переведите эти десятичные дроби в обыкновенные:
3,8; 0,75; 0,15; 1,4; 0,725; 0,012
Должны получиться вот такие ответы (в беспорядке!):
На этом и завершим. В этом уроке мы освежили в памяти ключевые моменты по дробям. Бывает, правда, что освежать особо нечего…) Если уж кто совсем крепко забыл, или ещё не освоил. .. Тем можно пройти в особый Раздел 555 . Там все основы подробненько расписаны. Многие вдруг всё понимать начинают. И решают дроби с лёту).
.. Тем можно пройти в особый Раздел 555 . Там все основы подробненько расписаны. Многие вдруг всё понимать начинают. И решают дроби с лёту).
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Тема : Понятие десятичной дроби.Чтение и запись десятичных дробей.
Цель урока : формирование навыков записи и чтения десятичных дробей, умений переводить обыкновенные дроби со знаменателями 10, 100, 1000 и т.д. в десятичную дробь.
Задачи:
— развивающие – развивать навыки самооценки и самоанализа учебной деятельности, развивать у учащихся математическую речь;
— воспитательные – воспитывать культуру математического мышления, умение работать самостоятельно.
3. Тип урока – урок закрепления знаний
4. Методы обучения: словесный, наглядный, практический
5. Формы работы учащихся – фронтальная, индивидуальная, групповая
6. Необходимое техническое оборудование – мультимедийный проектор, компьютер, экран
7. Учебно-методическое обеспечение : учебник «Математика 5», И. И. Зубарева, А. Г. Мордкович
Структура урока:
Орг. момент.
Повторение предыдущих тем, устная работа.
Математический диктант.
Физкультпауза.
Основная часть.
Рефлексия.
Домашнее задание.
Ход урока:
Орг. момент.
Взаимное приветствие учителя и учащихся.
Проверка рабочих мест.
Сообщение учащимся плана урока.
Как хорошо, что я попала именно к вам. Мне подсказали, что вы обязательно поможете в моем расследовании. ПОКАЗАНИЯ ПОТЕРПЕВШИХ.
ПОКАЗАНИЯ ПОТЕРПЕВШИХ.
Из двух пунктов А и В навстречу друг к другу выехали автомобиль и грузовик. Скорость автомобиля – 60 км/ ч, а скорость грузовика – 40 км/ ч. Через какое время они встретятся, если расстояние между пунктами 350 км?
— Рассмотрим решение.
1) 40 + 60 = 100 (км/ч) – общая скорость автомобилей (скорость сближения)
2) 350: 100 = 35 (ч)
Ответ: машины встретятся через 35 ч.
— Ребята, обратите внимание на все данные, и ответьте: «Не вызвал ли у вас сомнение этот результат?»
— Да, сомнение есть, в этой задаче время не может быть 35 часов.
— Итак, в результате решения была допущена ошибка. Каким должен быть ответ мы узнаем, проведя расследование и изучив все факты, документы и улики.
— Для нашего расследования я взяла лупу, весы и книги.
ПЕРВОЕ ЗАДАНИЕ. (улика первая)
Из данных чисел вычеркнуть:
Натуральные числа
Правильные дроби
Неправильные дроби
Смешанные числа
8 45/1000; 1000; 12; 3/2; 0,12; 1/6; 15/15; 30/24; 12/1000; 21,032; 1 2/3. Дробная часть десятичной дроби читается по последнему значащему разряду.
Дробная часть десятичной дроби читается по последнему значащему разряду.
Например:
0,3 — три десятых
0,75 — семьдесят пять сотых
0,000005 — пять миллионных.
Чтение целой части десятичной дроби такое же, как и натуральных чисел.
Например:
27,5 — двадцать семь…;
1,57 — одна…
После целой части десятичной дроби произносится слово «целых».
Например:
10.7 — десять целых семь десятых
0,67 — ноль целых шестьдесят семь сотых.
Десятичные знаки — это цифры дробной части. Дробная часть читается не по разрядам (в отличие от натуральных чисел), а целиком, поэтому дробная часть десятичной дроби определяется последним справа значащим разрядом.
В вычислениях чаще всего используются первые три разряда. Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.
1-й разряд после запятой — разряд десятых
2-й разряд после запятой — разряд сотых
3-й разряд после запятой — разряд тысячных
4-й разряд после запятой — разряд десятитысячных
5-й разряд после запятой — разряд стотысячных
6-й разряд после запятой — разряд миллионных
7-й разряд после запятой — разряд десятимиллионных
8-й разряд после запятой — разряд стомиллионных
Какие сведения получили вы о нашем объекте изучения?
Обратимся к архивным материалам.
Исследуем исторические улики. Как записывали эти дроби раньше?
В V веке китайский ученый Цзю-Чун-Чжи дробь вида 2,135436 записывал так:
2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок.
Узбекский ученый Джемшид Гиясэддин ал-Каши в книге
» Ключ к арифметике« (1424 г) показал запись дроби в одну строку числами в десятичной системе.
Для записи он применял то вертикальную черту,
то чернила черного и красного цветов.
В книге «Математический канон» французского математика Ф. Виета (1540-1603) десятичная дробь записана так 2 135436 — дробная часть подчеркивалась и записывалась выше строки целой части числа
1571 г. – Иоган Кеплер предложил современную запись десятичных дробей, т.е. отделение целой части запятой.
До него существовали другие варианты:
3,7 писали как 3(0)7 или 3\ 7 или разными чернилами целую и дробную части.
— Итак, опишите как выглядит десятичная дробь в настоящее время. А). Представьте в виде обыкновенной дроби числа:
А). Представьте в виде обыкновенной дроби числа:
0,13 6,013 0, 05 14,007 51, 3 830,0026
(Каждая группа получает одно число. Выполнив задание, проводит защиту своего ответа, дополняя собственным примером).
Б). Представьте в виде десятичной дроби число:
1 1 / 10 , 25 / 100 , 98 3 / 10 , 2 56 / 1000 , 75 108 / 10000
Р Б О А В
Расположите обыкновенные дроби в порядке возрастания.
БРАВО
4. РЕФЛЕКСИЯ.
— Наше следствие подходит к концу. Рассмотрены все материалы дела, сопоставлены факты, изучены документы.
— Вернемся к нашему нарушению.
— Каким должно быть число в задаче, для того чтобы получился правильный ответ? «Что потеряли в этом числе?» (ЗАПЯТУЮ)
— Какой правильный ответ?
— Как записать ответ обыкновенной дробью?
— Переведите в часы и минуты?
— Спасибо, молодцы. Снимаю перед вами шляпу. Мы справились с поставленной задачей.
5. Домашнее задание.
Подготовить сообщения по темам:
«История возникновения десятичных дробей»
«Где применяются десятичные дроби»
СПАСИБО ЗА УРОК.
Десятичная дробь отличается от обыкновенной дроби тем, что знаменатель у нее — это разрядная единица.
Например:
Десятичные дроби выделены из обыкновенных дробей в отдельный вид, что привело к собственным правилам сравнения, сложения, вычитания, умножения и деления этих дробей. В принципе, с десятичными дробями можно работать и по правилам обыкновенных дробей. Собственные правила преобразования десятичных дробей упрощают вычисления, а правила преобразования обыкновенных дробей в десятичные, и наоборот, служат связкой между этими видами дроби.
Запись и чтение десятичных дробей позволяет их записывать, сравнивать и производить действия над ними по правилам, очень похожим на правила действий с натуральными числами.
Впервые система десятичных дробей и действий над ними была изложена в XV в. самаркандским математиком и астрономом Джемшид ибн-Масудаль-Каши в книге «Ключ к искусству счета».
Целая часть десятичной дроби отделена от дробной части запятой, в некоторых странах (США) ставят точку. Если в десятичной дроби нет целой части, то перед запятой ставят число 0.
Если в десятичной дроби нет целой части, то перед запятой ставят число 0.
К дробной части десятичной дроби справа можно дописывать любое количество нулей, это величину дроби не изменяет. Дробная часть десятичной дроби читается по последнему значащему разряду.
Например:
0,3 — три десятых
0,75 — семьдесят пять сотых
0,000005 — пять миллионных.
Чтение целой части десятичной дроби такое же, как и натуральных чисел.
Например:
27,5 — двадцать семь…;
1,57 — одна…
После целой части десятичной дроби произносится слово «целых».
Например:
10.7 — десять целых семь десятых
0,67 — ноль целых шестьдесят семь сотых.
Десятичные знаки — это цифры дробной части. Дробная часть читается не по разрядам (в отличие от натуральных чисел), а целиком, поэтому дробная часть десятичной дроби определяется последним справа значащим разрядом. Разрядная система дробной части десятичной дроби несколько иная, чем у натуральных чисел.
- 1-й разряд после занятой — разряд десятых
- 2-й разряд после запятой — разряд сотых
- 3-й разряд после запятой — разряд тысячных
- 4-й разряд после запятой — разряд десятитысячных
- 5-й разряд после запятой — разряд стотысячных
- 6-й разряд после запятой — разряд миллионных
- 7-й разряд после запятой — разряд десятимиллионных
- 8-й разряд после запятой — разряд стомиллионных
В вычислениях чаще всего используются первые три разряда.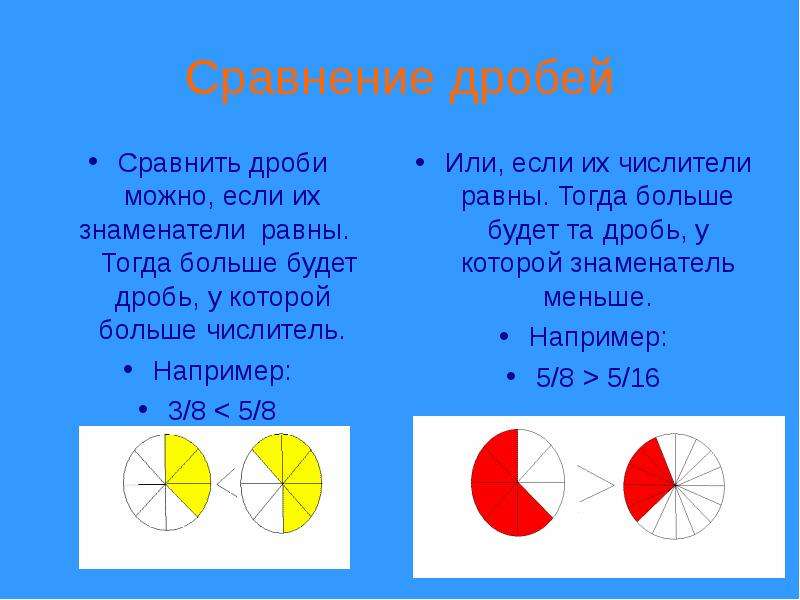 Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.
Большая разрядность дробной части десятичных дробей используется только в специфических отраслях знаний, где вычисляются бесконечно малые величины.
Перевод десятичной дроби в смешанную дробь состоит н следующем: число, стоящее до запятой записать целой частью смешанной дроби; число, стоящее после запятой — числителем ее дробной части, а в знаменателе дробной части записать единицу со столькими нулями, сколько цифр стоит после запятой.
Изучая царицу всех наук – математику, в определенный момент все сталкиваются с дробями. Хотя это понятие (как и сами виды дробей или математические действия с ними) совсем несложное, к нему нужно относиться внимательно, ведь в реальной жизни за пределами школы оно очень пригодится. Итак, давайте освежим свои знания о дробях: что это, для чего нужно, какие виды их бывают и как совершать с ними различные арифметические действия.
Ее величество дробь: это что такое
Дробями в математике называются числа, каждое из которых состоит из одной или более частей единицы. Такие дроби еще называют обыкновенными, либо простыми. Как правило, они записываются в виде двух чисел, которые разделены горизонтальной или слеш-чертой, она называется «дробной». Например: ½, ¾.
Такие дроби еще называют обыкновенными, либо простыми. Как правило, они записываются в виде двух чисел, которые разделены горизонтальной или слеш-чертой, она называется «дробной». Например: ½, ¾.Верхнее, или первое из этих чисел – это числитель (показывает, сколько взято долей от числа), а нижнее, или второе – знаменатель (демонстрирует, на столько частей разделена единица).
Дробная черта фактически выполняет функции знака деления. К примеру, 7:9=7/9
Традиционно обыкновенные дроби меньше единицы. В то время как десятичные могут быть больше ее.
Для чего нужны дроби? Да для всего, ведь в реальном мире далеко не все числа целые. К примеру, две школьницы в столовой купили в складчину одну вкусную шоколадку. Когда они уже собрались делить десерт, встретили подружку и решили угостить и и ее. Однако теперь необходимо правильно разделить шоколадку, если учесть, что она состоит из 12 квадратиков.
Поначалу девчонки хотели разделить все поровну, и тогда каждой бы досталось по четыре кусочка. Но, раздумав, они решили угостить подружку, не 1/3, а 1/4 шоколадки. А поскольку школьницы плохо изучали дроби, то они не учли, что при подобном раскладе в результате у них останется 9 кусочков, которые очень плохо делятся на двоих. Этот довольно простой пример показывает, насколько важно уметь правильно находить часть от числа. А ведь в жизни подобных случаев гораздо больше.
Но, раздумав, они решили угостить подружку, не 1/3, а 1/4 шоколадки. А поскольку школьницы плохо изучали дроби, то они не учли, что при подобном раскладе в результате у них останется 9 кусочков, которые очень плохо делятся на двоих. Этот довольно простой пример показывает, насколько важно уметь правильно находить часть от числа. А ведь в жизни подобных случаев гораздо больше.
Виды дробей: обыкновенные и десятичные
Все математические дроби делятся на два больших разряда: обыкновенные и десятичные. Об особенностях первого из них было рассказано в предыдущем пункте, так что теперь стоит уделить внимание второму.Десятичной называют позиционную запись дроби числа, которая фиксируется на письме через запятую, без черточки или слеша. Например: 0,75, 0,5.
Фактически десятичная дробь идентична обыкновенной, однако, в ее знаменателе всегда единица с последующими нулями – отсюда произошло и ее название.
Число, предшествующее запятой, – это целая часть, а все находящееся после — дробная.
 Любую простую дробь можно перевести в десятичную. Так, указанные в предыдущем примере десятичные дроби можно записать как обычные: ¾ и ½.
Любую простую дробь можно перевести в десятичную. Так, указанные в предыдущем примере десятичные дроби можно записать как обычные: ¾ и ½.Стоит отметить, что и десятичные, и обыкновенные дроби могут быть как положительными, так и отрицательными. Если перед ними стоит знак «-«, данная дробь отрицательная, если «+» — то положительная.
Подвиды обыкновенных дробей
Есть такие виды дробей простых.- Правильные. У них значение числителя всегда меньше, чем у знаменателя. Например: 7/8. Это правильная дробь, поскольку числитель 7 меньше, чем знаменатель 8. Неправильные. В таких дробях либо числитель и знаменатель равны между собою (8/8), либо значение нижнего числа меньше, нежели верхнего (9/8). Смешанная. Так называется правильная дробь, записанная вместе с целым числом: 8 ½. Она понимается как сумма этого числа и дроби. Кстати, довольно просто можно сделать так, чтобы на ее месте появилась неправильная дробь. Для этого 8 нужно записать как 16/2+1/2=17/2.Составные. Как понятно из названия, они состоят из нескольких дробных черт: ½ / ¾.
 Сократимые/несократимые. К ним может относиться как правильная, так и неправильная дробь. Все зависит от того, можно ли разделить числитель и знаменатель на одно и то же число. К примеру, 6/9 является сократимой дробью, ведь оба ее составляющих можно поделить на 3 и получится 2/3. А вот 7/9 относится к несократимым, поскольку 7 и 9 – простые числа, которые не имеют общего делителя и не могут быть сокращены.
Сократимые/несократимые. К ним может относиться как правильная, так и неправильная дробь. Все зависит от того, можно ли разделить числитель и знаменатель на одно и то же число. К примеру, 6/9 является сократимой дробью, ведь оба ее составляющих можно поделить на 3 и получится 2/3. А вот 7/9 относится к несократимым, поскольку 7 и 9 – простые числа, которые не имеют общего делителя и не могут быть сокращены.Подвиды десятичной дроби
В отличие от простой, десятичная дробь делится всего на 2 вида.- Конечная — получила такое название из-за того, что после запятой у нее ограниченное (конечное) число цифр: 19,25.Бесконечная дробь – это число с нескончаемым количеством цифр после запятой. К примеру, при делении 10 на 3 результатом будет бесконечная дробь 3,333…
Сложение дробей
Проводить различные арифметические манипуляции с дробями немного сложнее, чем с обычными числами. Однако, если усвоить основные правила, решить любой пример с ними не составит особого труда.Итак, чтобы сложить между собою дроби, прежде всего, нужно сделать так, чтобы у обоих слагаемых были одинаковые знаменатели.
 Для этого предстоит найти наименьшее число, которое способно поделиться без остатка на знаменатели слагаемых чисел.
Для этого предстоит найти наименьшее число, которое способно поделиться без остатка на знаменатели слагаемых чисел.Например: 2/3+3/4. Наименьшим общим кратным для них будет 12, следовательно, необходимо, чтобы в каждом знаменателе стояло это число. Для этого числитель и знаменатель первой дроби умножаем на 4, получается 8/12, аналогично поступаем со вторым слагаемым, но только множим на 3 – 9/12. Теперь можно легко решить пример: 8/12+9/12= 17/12. Получившаяся дробь – это неправильная величина, поскольку числитель больше знаменателя. Ее можно и нужно пребразовать в правильную смешанную, разделив 17:12= 1 и 5/12.
В случае, если слагаются смешанные дроби, сначала действия совершаются с целыми числами, а потом с дробными.
Если в примере присутствует десятичная дробь и обычная, необходимо, чтобы обе стали простыми, потом привести их к одному знаменателю и сложить. К примеру 3,1+1/2. Число 3,1 можно записать как смешанную дробь 3 и 1/10 или как неправильную — 31/10. Общим знаменателем для слагаемых будет 10, поэтому нужно умножить поочередно числитель и знаменатель 1/2 на 5, получается 5/10.
 Далее можно легко все высчитать: 31/10+5/10=35/10. Полученный результат — неправильная сократимая дробь, приводим ее в нормальный вид, сократив на 5: 7/2=3 и 1/2, или десятичной — 3,5.
Далее можно легко все высчитать: 31/10+5/10=35/10. Полученный результат — неправильная сократимая дробь, приводим ее в нормальный вид, сократив на 5: 7/2=3 и 1/2, или десятичной — 3,5.Если слагать 2 десятичные дроби, важно, чтобы после запятой было одинаковое количество цифр. Если это не так, нужно просто дописать необходимое количество нулей, ведь в десятичной дроби это можно сделать безболезненно. Например, 3,5+3,005. Чтобы решить это задание, нужно к первому числу прибавить 2 ноля и далее поочередно слагать: 3,500+3,005=3,505.
Вычитание дробей
Вычитая дроби, стоит поступать так же, как и при сложении: свести к общему знаменателю, отнять один числитель от другого, при необходимости перевести результат в смешанную дробь.Например: 16/20-5/10. Общим знаменателем будет 20. Нужно привести вторую дробь к этому знаменателю, умножив обе ее части на 2, получается 10/20. Теперь можно решать пример: 16/20-10/20= 6/20. Однако этот результат относится к сократимым дробям, поэтому стоит поделить обе части на 2 и получается результат – 3/10.

Умножение дробей
Деление и умножение дробей – значительно более простые действия, нежели сложение и вычитание. Дело в том, что, выполняя эти задания, нет необходимости искать общий знаменатель.Чтобы умножить дроби, нужно просто поочередно перемножить между собою оба числителя, а затем и оба знаменателя. Получившийся результат сократить, если дробь – это сократимая величина.
Например: 4/9х5/8. После поочередного умножения получается такой результат 4х5/9х8=20/72. Такая дробь сократима на 4, поэтому конечный ответ в примере – 5/18.
Как делить дроби
Деление дробей — тоже несложное действие, фактически оно все равно сводится к их умножению. Чтобы разделить одну дробь на другую, нужно вторую перевернуть и умножить на первую.Например, деление дробей 5/19 и 5/7. Чтобы решить пример, нужно поменять местами знаменатель и числитель второй дроби и умножить: 5/19х7/5=35/95. Результат можно сократить на 5 – получается 7/19.
В случае, если необходимо разделить дробь на простое число, методика немного отличается. Изначально стоит записать это число как неправильную дробь, а потом делить по той же схеме. Например, 2/13:5 нужно записать как 2/13: 5/1. Теперь нужно перевернуть 5/1 и умножить получившиеся дроби: 2/13х1/5= 2/65.
Изначально стоит записать это число как неправильную дробь, а потом делить по той же схеме. Например, 2/13:5 нужно записать как 2/13: 5/1. Теперь нужно перевернуть 5/1 и умножить получившиеся дроби: 2/13х1/5= 2/65.
Иногда приходится совершать деление дробей смешанных. С ними нужно поступать, как и с целыми числами: превратить в неправильные дроби, перевернуть делитель и умножить все. Например, 8 ½: 3. Превращаем все в неправильные дроби: 17/2: 3/1. Далее следует переворот 3/1 и умножение: 17/2х1/3= 17/6. Теперь следует перевести неправильную дробь в правильную – 2 целых и 5/6.
Итак, разобравшись с тем, что такое дроби и как можно с ними совершать различные арифметические действия, нужно постараться не забывать об этом. Ведь люди всегда более склонны делить что-то на части, нежели прибавлять, поэтому нужно уметь делать это правильно.
Дроби
Сколько равных частей целого
Разрежьте пиццу, и мы получим дроби:
| 1 / 2 | 1 / 4 | 3 / 8 |
(Половина) | (четверть) | (три восьмых) |
Верхнее число говорит, сколько у нас срезов.
Нижнее число говорит о том, сколько одинаковых кусочков пиццы было разрезано на .
Попробуйте сами:
Эквивалентные дроби
Некоторые дроби могут выглядеть по-разному, но на самом деле они одинаковые, например:
| 4 / 8 | = | 2 / 4 | = | 1 / 2 |
| (четыре восьмых) | (две четверти) | (Половина) | ||
| = | = |
Обычно лучше всего показывать ответ, используя самую простую дробь (в данном случае 1 / 2 ).Это называется Упрощение или Сокращение Дробь
Числитель/Знаменатель
Мы называем верхнее число Числитель , это количество частей у нас есть .
Назовем нижнее число Знаменатель , это количество частей целого делим на .
Числитель Знаменатель
Вам просто нужно запомнить эти имена! (Если вы забыли, просто подумайте «Вниз» — оминатор)
Добавление дробей
Легко складывать дроби с тем же знаменателем (то же самое нижнее число):
| 1 / 4 | + | 1 / 4 | = | 2 / 4 | = | 1 / 2 |
| (четверть) | (четверть) | (две четверти) | (Половина) | |||
| + | = | = |
Другой пример:
| 5 / 8 | + | 1 / 8 | = | 6 / 8 | = | 3 / 4 |
| + | = | = |
Сложение дробей с разными знаменателями
Но что делать, если знаменатели (нижние числа) не совпадают?
 .. Какие?
.. Какие?Мы должны как-то сделать знаменатели одинаковыми.
В данном случае это легко, потому что мы знаем, что 1 / 4 такой же, как 2 / 8 :
Три восьмых плюс две восьмых равно пяти восьмым
Существует два популярных метода приведения знаменателей числа к одному и тому же :
.(Они оба работают хорошо, используйте тот, который вам больше нравится.)
Другие вещи, которые мы можем делать с дробями
Мы также можем:
Посетите указатель фракций, чтобы узнать больше.
Основы дробей – Математика для торговли: Том 1
Что такое дробь? Вы когда-нибудь имели дело с дробями в школе или на работе? Итак, дробь — это часть (или часть) целого.
Допустим, вы заказали пиццу, и в ней всего 8 кусков. В тот день вы были голодны и съели 5 ломтиков, поэтому съели 5 из 8 ломтиков. Это можно представить в виде дроби.
Наша история о фракциях начинается с Эбигейл, Ханны и Наоми, учениц-электриков, которые одновременно учатся в школе и надеются вместе открыть компанию, как только получат билеты на электричество с красной печатью.
Начнем с пары определений. Каждая дробь состоит из двух частей: числителя и знаменателя. Давайте посмотрим на дробь, чтобы определить каждую.
Числитель : Число над чертой в дроби. Он показывает, сколько частей целого подсчитывается.
Знаменатель : Число под чертой в дроби. Он показывает, сколько всего частей в целом.
Если Эбигейл, Ханна и Наоми в конечном итоге станут владельцами компании, каждая из них будет владеть ⅓ этой компании. Каждый человек представляет 1 владельца, а вместе в компании 3 владельца.
Вот еще несколько примеров дробей:
[латекс]\БОЛЬШОЙ\dfrac{1}{2}\ \dfrac{3}{8}\ \dfrac{5}{16}\ \dfrac{4}{9}\ \dfrac{7}{15} \ \dfrac{77}{145}[/латекс]
Все приведенные выше примеры представляют собой типичные дроби, но мы не всегда видим дроби в такой форме.Есть еще два типа дробей, с которыми мы имеем дело: смешанные числа и неправильные дроби .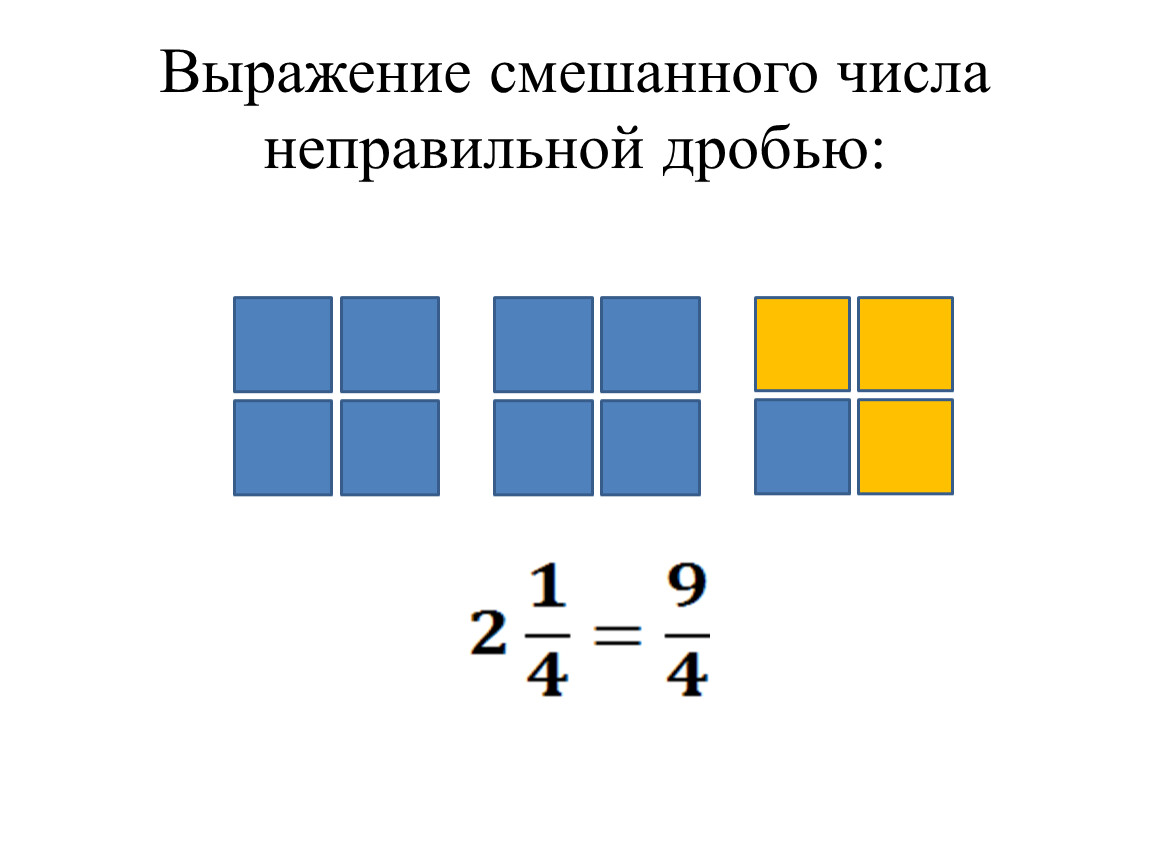
Смешанные номера
Допустим, трое учеников собираются однажды вечером, чтобы поговорить о будущем, и заказывают 2 пиццы, по 8 штук в каждой.
(Я знаю, что пиццы выглядят совершенно одинаково, но в этом вам придется мне поверить. Одно можно сказать наверняка: каждая пицца состоит из 8 ломтиков, и кто-то пошел дальше и попробовал обе пиццы на вкус.)
Нам нужно разбить это на части: всего у нас есть 2 пиццы, каждая из которых состоит из 8 ломтиков. Всего получается 16 ломтиков. Если ученики съедят 1 пиццу целиком, они съедят 8 из 8 кусков.
[латекс]\БОЛЬШОЙ\dfrac{8}{8}=1[/латекс]
Теперь предположим, что у одного из них есть еще один кусок второй пиццы. Теперь они съедят 1 целую пиццу плюс 1 кусочек.
[латекс]\БОЛЬШОЙ1+\dfrac{1}{8}=1\dfrac{1}{8}\longleftarrow\text{Смешанное число}[/latex]
Это так называемое смешанное число.Смешанное число можно определить следующим образом:
. Смешанное число : Сочетание целого числа и дроби.
Далее рассмотрим неправильные дроби.
Неправильные дроби
Неправильная дробь : Дробь, в которой числитель больше знаменателя.
Это означает, что число в верхней части дроби больше числа в нижней. Мы вернемся к нашему примеру с пиццей. Вместе ученики съели в общей сложности 9 ломтиков.Это составляет 1 целую пиццу плюс 1 кусок второй пиццы. В виде неправильной дроби количество съеденных пицц будет выглядеть так:
.[латекс]\БОЛЬШОЙ\dfrac{9}{8}[/латекс]
Теперь мы хотим преобразовать смешанное число в неправильную дробь, а затем сделать обратное, взять неправильную дробь и преобразовать ее обратно в смешанное число.
Превратите следующее смешанное число в неправильную дробь:
[латекс]\БОЛЬШОЙ1\dfrac{3}{4}[/латекс]
Шаг 1 : Преобразуйте целое число в дробь со знаменателем 4.
[латекс]\БОЛЬШОЙ1=\dfrac{4}{4}[/латекс]
Шаг 2 : Сложите две дроби вместе. Теперь нам придется немного забежать вперед, так как мы еще не рассмотрели добавление дробей. Я дам вам дешевую и простую версию здесь. Пока знаменатели одинаковы, у нас все хорошо. При сложении дробей мы просто сохраняем знаменатели одинаковыми и добавляем числители. (Мы подробно рассмотрим сложение дробей в следующей главе.)
Теперь нам придется немного забежать вперед, так как мы еще не рассмотрели добавление дробей. Я дам вам дешевую и простую версию здесь. Пока знаменатели одинаковы, у нас все хорошо. При сложении дробей мы просто сохраняем знаменатели одинаковыми и добавляем числители. (Мы подробно рассмотрим сложение дробей в следующей главе.)
[латекс]\БОЛЬШОЙ\dfrac{4}{4}+\dfrac{3}{4}=\dfrac{7}{4}[/latex]
Итак:
[латекс]\БОЛЬШОЙ1\dfrac{3}{4}=\dfrac{7}{4}[/латекс]
Еще один способ найти ответ:
Это может показаться немного запутанным, но следуйте за мной.Со смешанным числом 1 ¾ возьмите 4 и умножьте его на 1. Затем прибавьте 3, и вы получите 7. Это тот же ответ, просто другой способ его получения.
Попробуйте самостоятельно перейти от смешанного числа к неправильной дроби.
Измените следующую дробь на неправильную. Посмотрите видео ответ, чтобы увидеть, как вы это сделали.
[латекс]\БОЛЬШОЙ3\dfrac{3}{8}[/латекс]
Хорошо: надеюсь, вы справились с вычислением смешанных чисел и неправильных дробей. Но как насчет обратного? Мы также должны рассмотреть пример этого, а затем дать вам возможность проработать его самостоятельно.
Но как насчет обратного? Мы также должны рассмотреть пример этого, а затем дать вам возможность проработать его самостоятельно.
Замените следующую неправильную дробь смешанным числом:
[латекс]\БОЛЬШОЙ\dfrac{27}{6}[/латекс]
Шаг 1 : Узнайте, сколько раз 6 входит в число 27. Мы можем сделать это, используя деление в большую сторону. Хорошей новостью здесь является то, что мы уже прошли длинное деление в первой главе. Если вам нужно пересмотреть его, оглянитесь назад, чтобы увидеть, как это делается (см. Разделение целых чисел).
В итоге мы получаем, что 6 входит в число 27 четыре раза, а 3 остается. Таким образом, наше смешанное число становится:
.[латекс]\БОЛЬШОЙ4\dfrac{3}{6}[/латекс]
Попробуйте еще один тренировочный вопрос.
Замените следующую неправильную дробь смешанным числом. Посмотрите видео-ответ, чтобы узнать, как вы это сделали.
[латекс]\БОЛЬШОЙ\dfrac{17}{3}[/латекс]
Прежде чем мы перейдем к сложению и вычитанию дробей, мы должны коснуться другого понятия, известного как сокращение дробей. Уменьшение — это то, что мы делаем, когда хотим сделать уменьшенную версию дроби, которая по-прежнему имеет то же математическое значение, что и оригинал.
Уменьшение — это то, что мы делаем, когда хотим сделать уменьшенную версию дроби, которая по-прежнему имеет то же математическое значение, что и оригинал.
Вернемся к нашей пицце. Еще раз, у нас есть 8 кусочков на пиццу. Теперь, скажем, мы съедаем 4 таких ломтика. Мы съели:
Если бы вас спросили, сколько у вас пиццы, что бы вы ответили? Скажете ли вы: «Я съел 4 из 8 возможных кусочков» или «Я съел половину пиццы»? Думаю, мы все согласимся, что просто скажем, что съели половину пиццы, поскольку 4 куска составляют половину пиццы.Если бы мы записали половину как дробь, это выглядело бы так:
.[латекс]\БОЛЬШОЙ\dfrac{1}{2}[/латекс]
Тогда мы могли бы заключить, что две дроби математически представляют одно и то же, и это всего лишь два разных способа представления одного и того же. Вы можете посмотреть на это так: я вырезал два куска дерева. Один из них имеет длину 12 дюймов, а другой — 1 фут. Они одинаковой длины — просто их длины выражаются по-разному. Итак, в итоге у нас получается вот это:
[латекс]\БОЛЬШОЙ\dfrac{4}{8}=\dfrac{1}{2}[/латекс]
Мы уменьшили дробь с 4 на 8 до 1 на 2 без изменения фактического представленного значения.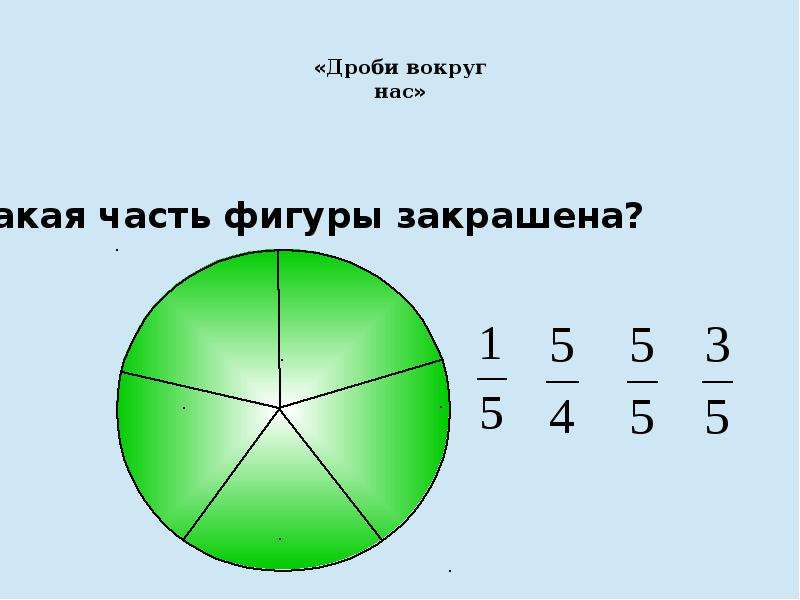 Как это было сделано математически, так это то, что мы взяли исходный числитель 4 и разделили его на 4. То, что делается с одной частью дроби, должно быть сделано и с другой, поэтому мы также разделили знаменатель 8 на 4, в результате чего дробь от 1 к 2.
Как это было сделано математически, так это то, что мы взяли исходный числитель 4 и разделили его на 4. То, что делается с одной частью дроби, должно быть сделано и с другой, поэтому мы также разделили знаменатель 8 на 4, в результате чего дробь от 1 к 2.
Выполнение одного и того же действия с числителем и знаменателем гарантирует, что исходная дробь и конечная дробь равны по значению.
Мы уменьшаем дроби, когда можем разделить одно и то же число без остатка как на числитель, так и на знаменатель.В нашем примере 4 можно разделить на оба. Обратите внимание, что число 2 также можно разделить как на числитель, так и на знаменатель. Если мы разделим оба на 2, мы получим:
Хотя с математической точки зрения это по-прежнему работает, мы часто хотим привести дробь к ее наименьшему выражению, то есть к точке, в которой ее уже нельзя уменьшить. Доля 2 к 4 может быть еще больше уменьшена до 1 к 2, так что мы могли бы проделать дополнительную работу, если бы захотели.
Давайте рассмотрим образ мыслей при сокращении дробей.Возьмите следующую дробь и уменьшите ее до наименьшего значения:
.[латекс]\БОЛЬШОЙ\dfrac{8}{12}[/латекс]
Шаг 1 : Здесь мы хотим взглянуть на числитель и знаменатель и определить, существует ли число, которое может входить в них оба. Возможно, будет проще, если вы запишете числа, начиная с 1, а затем решите, какие числа могут состоять как из 8, так и из 12.
Из этого можно сделать вывод, что наибольшее число, которое может входить как в 8, так и в 12, равно 4.
Шаг 2 : Разделите числитель и знаменатель на 4.
Вот и все: теперь дробь уменьшена до минимального значения. Когда вы закончите, всегда смотрите на ответ, просто чтобы убедиться, что определенно нет другого числа, которое могло бы войти в числитель и знаменатель, так как это означало бы, что дробь может быть уменьшена еще больше.
Приведенный выше пример довольно прост. Когда речь идет о больших числах, иногда проще решить вопрос за пару шагов, чтобы медленно уменьшить дробь.Взгляните на следующий пример, чтобы понять, что я имею в виду.
Когда речь идет о больших числах, иногда проще решить вопрос за пару шагов, чтобы медленно уменьшить дробь.Взгляните на следующий пример, чтобы понять, что я имею в виду.
Сократите следующую дробь до наименьшего значения:
[латекс]\БОЛЬШОЙ\dfrac{24}{168}[/латекс]
Шаг 1 : Определите, существует ли число, которое может входить как в числитель, так и в знаменатель. Если имеется более одного числа, используйте большее число.
Это немного сложнее, чем первый вопрос, так как числа намного больше и с ними сложнее работать. Возвращаясь к нашим таблицам умножения, мы видим, что 6, 8 и 12 составляют 24.Мы могли бы также сказать, что 24 идет на 24. Но как насчет 168? Что входит в это?
Одно мы знаем точно: 2 входит в оба числа, так почему бы нам не начать с того, что мы возьмем каждую часть дроби и разделим ее на 2. Если у вас возникли проблемы с делением 168 на 2 в уме, продолжайте и используйте ваш калькулятор.
Шаг 2 : Определите, можно ли еще уменьшить дробь. Мы видим, что мы снова можем разделить оба числа на 2.
Мы видим, что мы снова можем разделить оба числа на 2.
Шаг 3 : Повторите шаг 2 и определите, можно ли еще уменьшить дробь.На этот раз мы отмечаем, что 6 может входить как в 6, так и в 42, поэтому мы делим и числитель, и знаменатель на 6.
Вот и все: мы сократили эту крупную дробь до минимального значения всего за несколько шагов. Я признаю, что если бы мы использовали калькулятор для всей этой процедуры, мы могли бы получить ответ с меньшими усилиями, но это не главное. Делая это в долгосрочной перспективе, вы начинаете тренировать свой мозг в отношениях между числами. Когда вы лучше познакомитесь с числами, вы сможете различать закономерности и понимать отношения, формирующиеся в математике.Хотя поначалу это может занять немного больше времени, со временем отдача будет велика.
Попробуйте задать себе пару вопросов и посмотрите ответы в видео, чтобы узнать, как вы справились.
Приведите следующие дроби к наименьшему виду.
[латекс]\БОЛЬШОЙ\dfrac{15}{18}[/латекс]
[латекс]\БОЛЬШОЙ\dfrac{24}{36}[/латекс]
Использование дробей в повседневной жизни: примеры и важность — видео и расшифровка урока
Дроби
Дроби — это числа, которые не являются целыми и означают то, как они звучат: дробь или часть чего-то большего. Дроби имеют два числа: числитель (часть) и знаменатель (целое). Когда вы впервые изучали дроби, вы, вероятно, не видели смысла в их изучении, но знали ли вы, что дроби настолько полезны, что вы уже используете их в своей повседневной жизни?
Дроби имеют два числа: числитель (часть) и знаменатель (целое). Когда вы впервые изучали дроби, вы, вероятно, не видели смысла в их изучении, но знали ли вы, что дроби настолько полезны, что вы уже используете их в своей повседневной жизни?
Верно! В первом примере вы отправились за покупками и должны были использовать дроби для определения стоимости после скидки. А когда готовишь? Вы когда-нибудь хотели удвоить рецепт печенья, чтобы съесть больше печенья? Или как насчет времени? Здесь снова используются дроби.Давайте посмотрим на эти примеры.
Кулинария
Вы когда-нибудь пробовали печь, не следуя рецепту? Откройте любую кулинарную книгу, и вы увидите рецепты, полные дробей. Для выпечки вкусностей, таких как торты и печенье, требуется точное количество каждого ингредиента. Отсутствие даже одной столовой ложки чего-либо может резко изменить вкус чего-либо. Хотя следование рецепту кажется простым, что произойдет, если вы захотите удвоить его, чтобы сделать больше? Вот где дроби приходят, когда вы готовите.
Если в рецепте указано 2 ¼ стакана муки, и вы хотите удвоить его, знание дробей поможет вам определить, что вам нужно 4 ½ стакана муки. Или, если в рецепте указано разрезать плитку шоколада на четвертинки, знание ваших дробей поможет вам легко определить, что вам нужно четыре равных части или четыре ¼ части. В любом случае, вы используете дроби. Точно следуйте рецепту и добавьте нужное количество ингредиентов, и вы получите вкусный ужин и десерт.Но этого бы никогда не произошло, если бы у вас не было фракций, которые могли бы вам помочь.
Определение времени
Как и в выпечке, мы используем дроби для определения времени. Представьте, что часы — это целый круг, а каждая минута — это часть целого. Если вы хотите встретиться со своим другом в половине пятого, вы используете дроби для определения времени. Если вы печете (снова) и вам нужно проверять духовку 4 раза в час, вы используете дроби, чтобы определить, как часто вы должны проверять. 4/4 равно одному целому, 60 минут.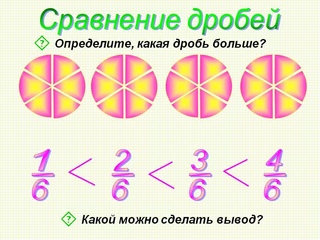 ¼ от 60 равняется 15 минутам.Проверка еды каждые 15 минут обеспечит вкусное угощение.
¼ от 60 равняется 15 минутам.Проверка еды каждые 15 минут обеспечит вкусное угощение.
В нашем первом примере мы уже ходили в торговый центр и обсуждали, насколько дроби являются важной частью покупок. Скидки записываются в процентах, которые на самом деле являются дробями. Слово процентов означает из ста, поэтому 20% на самом деле 20/100. Всякий раз, когда вам нужно рассчитать скидку, вы можете преобразовать свой процент в дробь, а затем умножить дробь на розничную цену.
Итоги урока
Давайте повторим.
Дроби — это числа, которые не являются целыми, но говорят вам, сколько у вас целого. Вот некоторые примеры дробей:
½, ¾, 5
Верхнее число называется числителем , а нижнее число — знаменателем . Дроби важны, потому что они говорят вам, какая часть целого вам нужна, есть или чего вы хотите. Фракции используются в выпечке, чтобы сказать, сколько ингредиента нужно использовать. Дроби используются для определения времени; каждая минута — это часть часа. Наконец, дроби используются для определения скидок, когда идет распродажа.
Наконец, дроби используются для определения скидок, когда идет распродажа.
| Заблуждения | Примеры предотвращения или исправления |
|---|---|
Некоторые студенты путают термины числитель и знаменатель . | Объясните учащимся, что обозначают числители и знаменатели. |
Некоторые ученики считают, что дроби должны быть меньше 1. Они считают, что числитель должен быть меньше знаменателя; иначе не было бы достаточного количества штук. |
|
Некоторые учащиеся считают маленькие разделительные знаки (галочки) на числовой прямой, а не интервалы.
| На каждом интервале нарисуйте тонкие овалы. Другой метод заключается в том, чтобы учащиеся поместили палец на 0, двигали пальцем вправо и считали вслух каждую дробную часть, читая каждую галочку. |
Некоторые учащиеся считают, что дроби эквивалентны только тогда, когда они выглядят одинаково или имеют одинаковое количество выбранных частей. |
|
Некоторые учащиеся считают, что выполнение операции всегда изменяет значение исходной величины, даже при умножении или делении на 1. |
|
Некоторые учащиеся выполняют операцию только над числителем при работе с дробями.
| Объясните учащимся, что выполнение операции только над числителем отличается от применения свойства мультипликативной идентичности и приводит к изменению дробного значения и его положения на числовой прямой. |
Некоторые учащиеся ошибочно используют аддитивные рассуждения вместо мультипликативных при определении или создании эквивалентных дробей. Например, учитывая , эти учащиеся прибавляют 8 к числителю и знаменателю, чтобы получить , вместо того, чтобы умножать и числитель, и знаменатель на 8 (умножая всю дробь на 1), чтобы получить . |
|
Что означают дробные показатели? | Бретт Берри | Математические приемы
Дроби как показатели степени?! Не волнуйтесь, это просто условное обозначение степеней и корней.Как только вы это поймете, они просты, как пирог! Проверьте это.
Важной особенностью здесь является корневой индекс . Помните, что корневой индекс говорит нам , сколько раз наш ответ нужно умножить на себя, чтобы получить подкоренное число.
Дробная экспонента — альтернативное обозначение для совместного выражения степеней и корней. Например, следующие эквивалентны.
Запишем степень в числителе и индекс корня в знаменателе .Если питание не подается, напишите «1» в числителе в качестве заполнителя.
Чему будет эквивалентно следующее в радикальной записи?
Для наших целей не имеет значения, записываете ли вы вторую степень на 8 или на кубический корень.
Поскольку кубический корень из 8 равен 2, я предпочитаю сначала взять корень, а затем применить мощность.
Конечно, другой порядок дает тот же результат.
Чему соответствует следующее выражение в экспоненциальной записи?
Это эквивалентно 2 в степени 5/4.
Если мы хотим, мы можем манипулировать приведенным выше выражением еще больше. Начните с осознания того, что 5/4 эквивалентно 1 + 1/4.
Отсюда отбросьте степень 1, так как в ней нет необходимости, и перепишите степень 1/4 как корневой индекс 4. Также не стесняйтесь отбрасывать символ умножения.
Много раз студенты приходили ко мне в замешательстве, потому что не могли понять, что они делают неправильно; их ответ не соответствовал ключу ответа. Часто ключ ответа еще больше упрощал ответ или писал его в формате, отличном от формата работы студента. Ученик был прав, но не знал этого!
Ученик был прав, но не знал этого!
Спасибо за внимание! Дополнительные примеры, в том числе примеры с алгебраическими выражениями, см. в видео, указанном выше.
Решение многошаговых линейных уравнений с дробями
Нам нужно более двух операций, чтобы решить линейное уравнение . Использовать обратные операции для отмены каждой операции в обратном порядке.
Если уравнение содержит дроби, умножьте обе части уравнения на наименьший общий знаменатель (ЖК-дисплей) для очистки фракций.
Этапы решения многошагового уравнения:
Шаг 1 Очистить уравнение дробей.
Шаг 2 Использовать Распределительное свойство чтобы убрать скобки с каждой стороны.
Шаг 3 Объединение подобных терминов с каждой стороны.
Шаг 4 Отменить сложение или вычитание.
Шаг 5 Отменить умножение или деление.
Пример:
Решать 2 у 3 + у 2 знак равно 7 .
Решение
Наименьший общий знаменатель (LCD) в этом случае равен 6 . Итак, умножьте обе части уравнения на 6 .
6 ( 2 у 3 + у 2 ) знак равно 6 ( 7 )
Использовать распределительный закон в левой части уравнения.
6 ( 2 у 3 ) + 6 ( у 2 ) знак равно 6 ( 7 )
Умножить.
4 у + 3 у знак равно 42
Соедините подобные термины.
7 у знак равно 42
Отменить умножение.Разделите каждую сторону на 7 .
7 у 7 знак равно 42 7
Упрощать.
у знак равно 6
Калькулятор дробей
Использование калькулятора
Используйте этот калькулятор дробей для сложения, вычитания, умножения и деления дробей.Ответы представляют собой дроби в наименьшем выражении или смешанные числа в сокращенной форме.
Введите правильные или неправильные дроби, выберите математический знак и нажмите «Рассчитать». Это калькулятор дробей с шагами, показанными в решении.
Это калькулятор дробей с шагами, показанными в решении.
Если у вас есть отрицательные дроби, поставьте знак минус перед числителем. Итак, если одна из ваших дробей равна -6/7, вставьте -6 в числитель и 7 в знаменатель.
Иногда в математических задачах встречается слово «из», например, Что такое 1/3 от 3/8? На средства нужно умножить, поэтому нужно решить 1/3 × 3/8.
Для выполнения математических операций со смешанными числами (целыми числами и дробями) используйте Калькулятор смешанных чисел.
Математика дробей с разными знаменателями
Есть 2 случая, когда вам нужно знать, имеют ли ваши дроби разные знаменатели:
- если вы складываете дроби
- если вы вычитаете дроби
Как складывать и вычитать дроби
- Найдите наименьший общий знаменатель
- Вы можете использовать ЖК-калькулятор для нахождения наименьшего общего знаменателя набора дробей
- Для первой дроби найдите, на какое число нужно умножить знаменатель, чтобы получить наименьший общий знаменатель
- Умножьте числитель и знаменатель первой дроби на это число
- Повторите шаги 3 и 4 для каждой фракции
- Для уравнений сложения добавьте числители дробей
- Для уравнений вычитания вычтите числители дробей
- Преобразование неправильных дробей в смешанные числа
- Сократить дробь до наименьшего члена
Как умножать дроби
- Умножить все числители вместе
- Умножить все знаменатели вместе
- Уменьшить результат до минимального значения
Как делить дроби
- Перепишите уравнение, как в «Сохранить, изменить, перевернуть»
- Сохранить первую дробь
- Заменить знак деления на умножение
- Переверните вторую дробь, поменяв местами верхние и нижние числа
- Умножить все числители вместе
- Умножить все знаменатели вместе
- Уменьшить результат до минимального значения
Формулы дробей
Существует способ складывать или вычитать дроби, не находя
наименьший общий знаменатель (LCD). Этот метод предполагает перекрестное умножение дробей. См. формулы ниже.
Этот метод предполагает перекрестное умножение дробей. См. формулы ниже.
Возможно, вы обнаружите, что проще использовать эти формулы, чем заниматься математикой, чтобы найти наименьший общий знаменатель.
Формулы для умножения и деления дробей следуют тому же процессу, что описан выше.
Добавление дробей
Формула сложения дробей:
\( \dfrac{a}{b} + \dfrac{c}{d} = \dfrac{ad + bc}{bd} \)
Пример шагов:
\( \dfrac{2}{6} + \dfrac{1}{4} = \dfrac{(2\times4) + (6\times1)}{6\times4} \)
\( = \dfrac{14}{24} = \dfrac{7}{12} \)
Вычитание дробей
Формула вычитания дробей:
\( \dfrac{a}{b} — \dfrac{c}{d} = \dfrac{ad — bc}{bd} \)
Пример шагов:
\( \dfrac{2}{6} — \dfrac{1}{4} = \dfrac{(2\times4) — (6\times1)}{6\times4} \)
\( = \dfrac{2}{24} = \dfrac {1}{12} \)
Умножение дробей
Формула умножения дробей:
\( \dfrac{a}{b} \times \dfrac{c}{d} = \dfrac{ac}{bd} \)
Пример шагов:
\( \dfrac{2}{6} \times \dfrac{1}{4} = \dfrac{2\times1}{6\times4} \)
\( = \dfrac{2}{24} = \dfrac {1}{12} \)
Деление дробей
Формула деления дробей:
\( \dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{ad}{bc} \)
Пример шагов:
\( \dfrac{2}{6} \div \dfrac{1}{4} = \dfrac{2\times4}{6\times1} \)
\( = \dfrac{8}{6} = \dfrac{4}{3} = 1 \dfrac{1}{3} \)
Связанные калькуляторы
Для выполнения математических операций над дробями смешанных чисел используйте наш
Калькулятор смешанных чисел. Этот калькулятор также может преобразовать неправильные дроби в смешанные числа и показать затраченную работу.
Этот калькулятор также может преобразовать неправильные дроби в смешанные числа и показать затраченную работу.
Если вы хотите упростить отдельные дроби до минимума, используйте наш Упрощенный калькулятор дробей.
Объяснение того, как разложить числа на множители для нахождения наибольшего общего делителя (НОД), см. Калькулятор наибольшего общего фактора.
Если вы упрощаете большие дроби вручную, вы можете использовать Длинное деление с калькулятором остатков, чтобы найти целое число и значения остатка.
Примечания
.


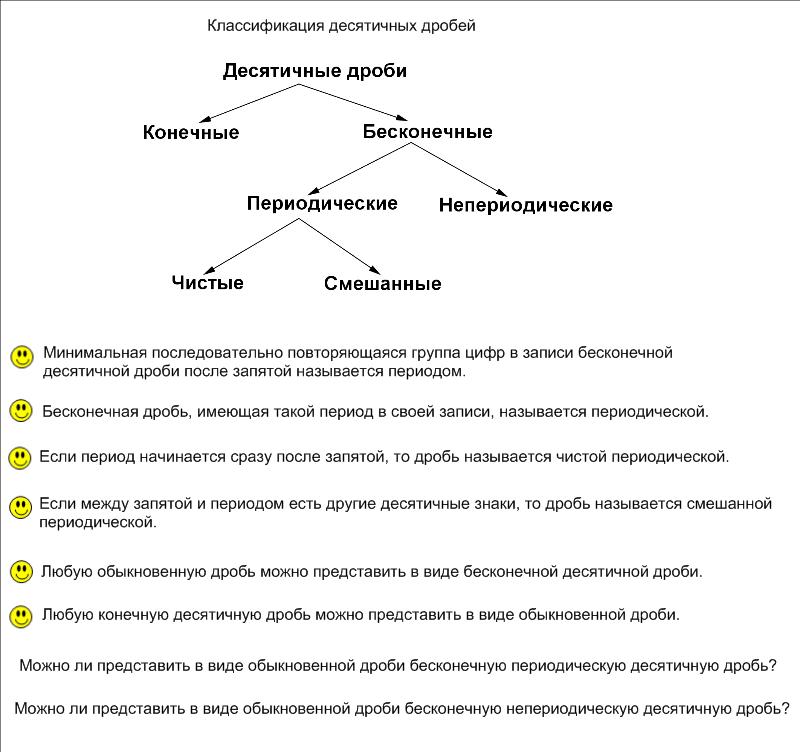

 Объясните учащимся, что рациональные числа включают в себя целые числа.
Объясните учащимся, что рациональные числа включают в себя целые числа.
 Используйте манипуляторы по мере необходимости.
Используйте манипуляторы по мере необходимости.